『Learning the Structure of Generative Models without Labeled Data』阅读笔记
优化一个不同的目标函数，可以扩大对许多潜在不相关依赖项的学习：
Inferring Generative Model Structure with Static Analysis-2017【论文理解】
真实的标签true label在生成模型中是一个隐变量。
对于一个数据点 $x_i$，它的真实标签为 $y_i\in-1,1$，有 n 个标记函数LFs，然后对 $x_i$ 就可以得到n个预测结果组成的标注向量 $\Lambda_i=\Lambda_{i1},…\Lambda_{in}$ 从n个结果中我们可以通过生成模型得到一个最终的结果 $\Lambda_i\in-1,0,1$ 三个值分别对应false，不确定，true。
目标是估计一个概率模型,生成labeling-function输出标注矩阵 $\Lambda \in {-1,0,1}^{m\times n}$。
假设n个结果 $\Lambda_i=\Lambda_{i1},…\Lambda_{in}$ 都条件独立于 $y_i$ ，$\Lambda_i$ 与 $y_i$ 之间就存在n个准确性依赖关系，那么估计每个结果相对于真实标签的一个准确率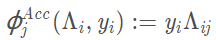
，acc因子函数建模每个标签函数 $\lambda_j$ 的准确性。
将此结构称为条件独立模型，并将其指定为：(类似于用内积表示相似度，所以设计成{-1,0,1})
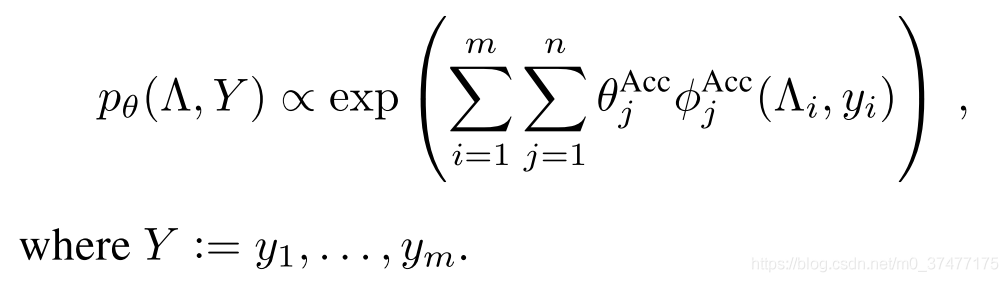
通过最小化的边际负对数似然估计参数，参数表示每个标记函数对数据 $y_i$ 的标注的权重(信心)，
专有名词
- 监督的准确性
- marginal pseudolikelihood
- sub-linearly
- EM算法
- log marginal pseudolikelihood
- 在线截断梯度法online truncated gradient method——https://zr9558.com/2016/01/12/truncated-gradient/
- 易辛模型
Abstract
生成模型的依赖关系结构 generative model’s dependency structure直接影响估计标签的质量，但是自动选择一个结构在没有标签数据情况下是一个明显的挑战。
我们提出了一种结构估计方法，可以最大程度地提高观测数据的L1正则的边际伪似然概率。
我们的分析表明， for a broad class of models，识别真实结构true structure所需的未标记数据量随着可能的依赖dependencies的数量按次线性缩放 scales sub-linearly 。
1. Introduction
人们越来越有兴趣使用生成模型从弱监督源中综合训练数据，such as heuristics, knowledge bases, and weak classifiers trained directly on noisy sources。这种方法不是将训练标签视为金标准输入，而是将训练集的创建建模为一个过程，以便大规模生成训练标签。数据点的真实类标签被建模为隐变量，该变量生成可观察到的有噪声的标签。将生成模型的参数拟合到未标记的数据后，得到该隐变量的分布，从分布中推断出真实标签。
此类生成模型的此类生成模型的结构直接影响推断的真实标签，先前的工作假设该结构是用户指定的（Alfonseca等，2012； Takamatsu等，2012； Roth＆Klakow，2013b； Ratner等，2016）
一种想法是假设在给定 latent class label，supervision sources是条件独立的。但是，统计上的依赖关系在实践中很常见，不考虑它们会导致对监督准确性 accuracy of the supervision的误判。我们一般不能依靠用户来指定生成模型的结构，因为对某些数据集进行监督的启发式方法和分类器可能是独立的，而对其他数据集则不是。因此，我们寻求一种仅从弱监督源自动学习生成模型的结构的有效方法
在有监督的环境中对结构学习进行了很好的研究 (e.g.,Meinshausen & B ̈uhlmann,2006;Zhao & Yu,2006;Ravikumar et al.,2010, see also Section6), 因为真正的类别标签是潜在的，所以要获得用于弱监督的生成模型的结构具有挑战性。尽管我们可以使用随机梯度下降和吉布斯采样来学习给定结构的生成模型参数，但是对所有可能的依赖关系建模并不能作为模型选择的替代方法(对所有可能的依赖关系建模成为性能瓶颈)。例如，为一个规模最大的100个弱监督源的问题估计所有可能的相关性需要40分钟。（为进行比较，我们提出的方法在15秒内解决了相同的问题。）随着用户发展其监督启发式方法，重新运行参数学习以识别依赖项成为一个瓶颈。
我们提出一种估计器estimator，以在不使用任何标记训练数据的情况下学习生成模型的依赖结构 learn the dependency structureof a generative model。我们的方法独立地 maximizes 每个监管源的输出的“ L1-正则化边际伪似然”，选择了那些非零权重的依赖。估算器类似于逻辑回归的最大似然法——对数最大似然，除了我们将潜在类标签的不确定性边缘化了。由于伪似然概率是一个自由变量的函数，并且对另一个变量进行了边际化，因此我们可以精确计算边际伪似然的梯度，从而避免了像最大似然估计那样使用Gibbs采样逼近梯度的需要。
我们的分析表明，对于一类广泛的模型，识别真实结构所需的数据量以亚线性方式按比例缩小。从直觉上讲，这是基于这样的事实，即当有足够多的优于随机性的监督资源可用时，就可以学习生成模型的参数。与随机猜测相比，有了足够的信号来更好地估计潜在类别标签 latent class labels ，可以对那些估计进行完善，直到确定模型为止
2. Background
在数据编程中，弱监督源被编码为labeling functions，即标记数据点（或弃权）的启发式方法。生成概率模型适合于估计标记函数的准确性以及任何用户的输出间用户指定的统计依赖性的强度。在此模型中，数据点的真实类标签是一个潜在变量，它会生成标签函数输出。拟合生成模型的参数后，可以估计潜在的真实标签上的分布，并通过将与该分布有关的预期损失最小化来用于训练判别模型。
我们首先通过为每个指定的数据点 $x_i$ a latent random variable $y_i\in\{-1,1\}$ 作为它的true label。例如，在信息提取任务中， $x_i$ 可能是一段文字，那么 $ y_i$ 可以代表是否提及某家公司（实体标签）。或者，$x_i$ 可能是一个更复杂的结构，例如文档中的规范标识符的元组 a tuple of canonical identifiers 和相关提及，然后 $ y_i$ 可以表示文档中是否表达了对该元组的感兴趣关系（关系提取
我们没法直接获得 $ y_i$ （即使在训练时），但是我们有用户提供的n个标注函数$\lambda_1,\lambda_2,…\lambda_n$，可以将其应用于 $x_i$ 以产生输出$\Lambda_1,\Lambda_2,…\Lambda_n$。例如，对于上面提到的company-tagging task ，标注函数可以将常规表达式 .+\sInc 应用于文本范围，并返回是否匹配。每个$ \Lambda_{i,j}\in\{-1,0,1\}$，分别对应于false，abstain和true。扩展到多类情况很简单。
Our goal is to estimate a probabilistic model that generates the labeling-function outputs $\Lambda_{i,j}\in\{-1,0,1\}^{m\times n}$ 。一个常见的假设是：在给定真实标签下，输出是条件独立的，并且$\Lambda$和 $y$ 之间的关系由n个accuracy dependencies来控制
使用一个参数建模每个标注函数 $\lambda_i$ 的准确性，我们将此结构称为条件独立模型，并将其指定为：
我们估计参数 $\theta$ by minimizing the negative log marginal likelihood $p_{\theta}(\bar\Lambda)$, $\bar\Lambda$是观察到的标记函数输出矩阵。
使用随机梯度下降法可以直接优化，上式对$\theta_j^{Acc}$ 的梯度是联合分布 $p_{\theta}$ 的相应充分统计量和在观察矩阵$\bar\Lambda$的条件下的同个分布即$p_{\theta|\bar\Lambda}$
$\sum_{i=1}^m(E_{\Lambda,Y \text{~}\theta}[\phi_j^{Acc}(\Lambda_i,y_i)]- E_{Y\text{~}\bar\Lambda|\theta}[\phi_j^{Acc}(\bar\Lambda_i,y_i)])$
在实践中，我们可以交错采样interleave samples以非常紧密地估计梯度和梯度步长，在对每个变量$\Lambda_{ij}$或者$y_i$进行一次采样后，走一个梯度步长，similarly to contrastive divergence (Hinton,2002).(可以不用蒙特卡洛采样，吉布斯采样——)
条件独立模型是一种常见的假设，当前使用更复杂的生成模型需要用户指定其结构。在本文的其余部分，我们将解决从观察$\bar\Lambda$自动识别依赖结构dependency structure的问题，而无需观察$Y$
3. Structure Learning without Labels
统计依赖性在弱的监督源中自然而然地出现。在数据编程中，用户通常会编写带有直接相关输出的labeling functions ，甚至是故意设计的，narrow的，更精确的启发式方法来增强其它的labeling functions。为了解决这个问题，我们将条件独立模型泛化到为具有附加依赖性的因子图factor graph ，包括将每个数据点$x_i$和 label $y_i$的多个标记函数输出multiple labeling function outputs连接起来的高阶因子。我们将通用模型指定为
这里$T$是感兴趣的依赖项类型的集合，$S_t$ 是index tuples的集合，指出参与每个类型依赖项dependency of type $t\in T$的 labeling function。
标准的依赖类型 correlation 定义为：
我们将这种依赖关系称为标记函数之间的成对依赖关系，因为它们仅依赖于两个标记函数输出。我们还可以考虑涉及更多变量的高阶相依性，例如依赖类型 conjunction:
估计the structure of the distribution $p_{\theta}(\Lambda,Y)$具有挑战性，因为$Y$是latent; we never observe its value,even during training。因此，我们必须和边际概率marginal likelihood $p_{\theta}(\Lambda)$。jointly学习生成模型的参数需要Gibbs采样来估计梯度。由于可能的dependencies的数量增加至少是标注函数数量的平方次，this heavyweight approach to learning does not scale （请参见第5.2节）
3.1. Learning Objective
我们可以扩大对许多潜在不相关依赖项的学习，通过优化另一个目标：the log marginal pseudolikelihood of the outputs of a single labeling function $\lambda_i$, 以其他的 labeling function输出作为条件 conditioned on $\lambda_{\setminus i}$, 用L1正则引入稀疏性，引入了特征选择
(边际概率，EM算法)
Objective:
$\varepsilon >0$ 是超参
通过取这个条件概率 $\log\sum_{y_i}p_{\theta}(\bar\Lambda_{ij},y_i\mid\bar\Lambda_{i\setminus j})$ ,我们确保可以在多项式时间内根据标记函数，数据点和possible dependencies;的的数量来计算梯度；无需任何sampling or variational approximations。
对数边际伪似然的梯度是两个期望之间的差：以所有标记函数(除了$\lambda_j$)为条件的充分统计量和以所有标记函数为条件的充分统计量：
3.2. Implementation
这是一种随机梯度下降（SGD）例程。在每次下降中，为单个数据点估计梯度，可以通过封闭式算出。使用SGD有两个优点：首先，它仅需要一阶梯度信息，诸如内点法interior-point（Koh et al。，2007）之类的用于1-正则回归的其他方法通常需要计算二阶信息。其次，观察结果$\bar\Lambda$可以逐步进行处理，由于数据编程对未标记的数据（通常是大量的）进行操作，因此 scalability 泛化能力至关重要。为了实现SGD中的1正则化，我们使用了在线截断梯度法online truncated gradient method（Langford等，2009)
在实践中，我们发现唯一需要调整的参数是$\varepsilon$，它控制the threshold and regularization strength. 较高的值会在所选结构中引起更大的稀疏性。对于其他参数，我们在所有实验中都使用相同的值：步长$\eta$=$m^{-1}$，epoch count T = 10，truncation frequency 窗口大小K = 10。
4. Analysis
我们保证Algorithm1成功恢复确切的依赖结构的可能性。我们首先为所有可能的依赖关系（包括成对依赖关系和高阶依赖关系）提供一般恢复保证。但是，在许多情况下，不必对标注函数的行为进行较高的依赖性的建模higher-order dependencies are not necessary to model the behavior of the labeling functions。实际上，正如我们在第5.3节中所演示的那样，在许多有用的模型中，只有准确性相关性和成对相关性accuracy dependencies and pairwise correlation。在这种情况下，作为一般结果的推论，我们证明所需样本的数量在可能的依存关系数量上是次线性的，更具体地说是$O(nlogn)$
前面针对监督案例的分析不能直接迁移到非监督情况，因为不再是凸问题。例如，analysis of an analogous method相同方法 for supervised Ising models（Ravikumar等，2010）依赖于拉格朗日对偶性和紧密对偶性缺口tight duality gap，这对于我们的估计问题不成立。取而代之的是，我们推断出参数空间的一个区域，在该区域中，我们可以估计出足够好，从而最终可以得到the true model。
现在我们陈述the conditions necessary for our guarantees。首先是两个必需的standard conditions 来保证可以用任意数量的样本恢复依赖结构：
一，我们必须有一些可行的参数集合$\Theta\subset R^M$。
二，真正的model在 $\Theta$ 里
这意味着对于每个标记函数，使用它将比不使用时更好地估计依赖项。它类似于对数据编程中的参数学习进行分析的假设
5. Experiments
我们将我们的方法作为开源框架Snorkel1的一部分进行实施，并通过三种方式对其进行评估。首先，我们使用合成数据来测量返回精确相关结构的概率如何受到问题参数的影响，从而确认我们的分析表明其样本复杂度在可能的依赖项数量上是次线性的。事实上，我们发现在实践中，样本的复杂度低于理论上的保证率，与在完全监督的结构学习中所看到的率相匹配。其次，我们将我们的方法与通过参数学习估计结构的所有可能依赖项进行了比较。我们的方法更快，更准确，平均选择了1/4倍的外部相关性。第三，我们将我们的方法应用于使用数据编程构建的实际应用程序中，例如从PubMed期刊摘要和硬件规格表中提取信息。在这些应用程序中，用户未指定标注函数之间的任何依赖关系，但这些依赖性自然产生，例如由于显式组成，放松或加强了标签功能启发式算法 explicit composing, relaxing, or tightening of labeling function heuristics；相关的远程监管资源；或多个并发的开发人员编写标注函数。我们表明，学习这种结构比条件独立模型可以提高性能，平均提高1.5 F1点。
5.1. Sample Complexity
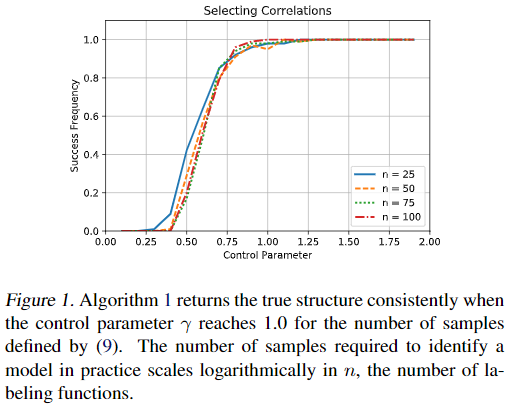
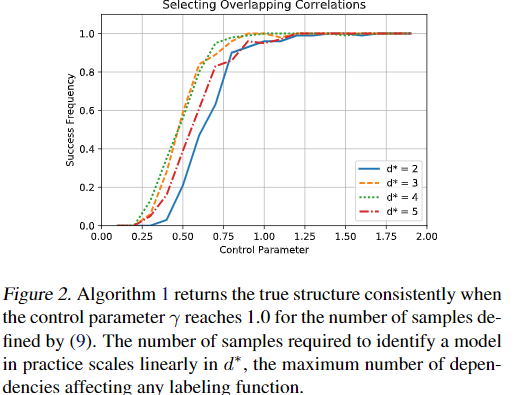
我们测试了Algorithm1返回正确的相关结构的概率如何取决于真实分布。我们在第4节中的分析保证，样本复杂性最差在n个标注函数的O（nlogn）阶上增长。在实践中，我们发现结构学习的效果要比保证率好，线性地取决于真实相关性的数量，对数取决于可能的相关性的数量。这与Ising models 的完全监督结构学习中观察到的行为相匹配（Ravikumar等人，2010），这也比最著名的理论保证更严格。
我们首先测试标注函数数量变化的影响。 For $n\in\{25,50,75,100\}$
设置两对标注函数be correlated with$\theta_{jk}^{Cor}=0.25$， 设置$\theta_{j}^{Acc}=1.0$ 对所有 j
然后，我们为100多个试验的每个设置生成m个样本。
5.2. Comparison with Maximum Likelihood
5.3. Real-World Applications
考虑了三个任务：从科学文献中提取特定疾病的提及mentions of specific diseases（疾病标记）；从科学文献中摘录有关化学物质诱发疾病的记载mentions of chemicals inducing diseases(Chemical-Disease)；并从PDF零件表中提取关于电子设备极性的说明（设备极性）。在前两个应用中，我们考虑一个训练集包含500个来自PubMed的未标记摘要，在第三情况下，我们考虑了由混合文本和表格数据组成的100个PDF parts sheets 。我们使用手工标记的测试集来评估 on the candidate-mention-level performance，即分类器在给定 a set of candidate mention的情况下识别特定实体或关系的正确提及的准确性。例如，在化学疾病中，我们将通过 标准预处理工具 确定的所有 共生化学疾病提及对 co-occurring chemical-disease mention pairs 视为候选。
我们看到，对标记函数之间的相关性进行建模可以提高性能，这似乎与源总数相关correlated with the total number of source。不同的源使用不同的匹配启发式方法检查 参考疾病本体的特定子树的成员for membership in specific subtrees of a reference disease ontology，标注函数在检查本体的相同子树使会发生重叠
检查化学疾病任务后，我们发现我们的方法可以识别明显是真实的相关性和更微妙的相关性，例如，我们的方法将学习labeling functions 之间的依赖性，这些labeling functions 是彼此的组成部分，例如一个标签函数检查模式$\text{[CHEM] induc.* [DIS]}$ 而另一种标注函数，在已知化学-疾病关系的外部知识库中检查此模式以及成员身份。
我们的方法还学习了更细微的相关性：例如，它选择了一种标记函数，该标记函数在 包含候选物 的 chemical and disease mentions 之间检查一个chemical mention是否存在，而一个标记函数则检查$\text{.*-induced}$出现在两者之间。
7. Conclusion and Future Directions
我们表明，学习生成模型的结构可以实现更高质量的数据编程结果。我们的结构学习方法也比最大似然方法快100倍。如果要通过数据编程和其他形式的弱监督来简化机器学习工具的开发，则必须以最少的用户干预为生成模型选择准确的结构。有趣的问题仍然存在。可以提高定理1的担保以获得更高阶的依赖性以匹配推论2的成对情况吗？初步实验表明它们在实践中以相似的速率收敛