Guo Jiazhen's Blog
0%

A Short Introduction to Probabilistic Soft Logic 阅读笔记

Posted on Edited on In , , Views: Valine:
Symbols count in article: 7.7k Reading time ≈ 7 mins.
概率软逻辑(Probabilistic soft logic PSL)为用户之间的不同类型的关系（例如友谊或家庭关系）建模，而且还可以对多种相似性概念。当样本不符合IID，可用PSL来建模

『』阅读笔记

project address

code

介绍视频

统计关系学 statistical relational learning

专有名词

rule learning 规则学习

first order logic rules ——一阶逻辑)

image-20200726120840738

Atom 原子公式：命题逻辑)

  1. collective classification
  2. ontology alignment
  3. personalized medicine
  4. opinion diffusion
  5. trust in social networksolollllllllllllllllllll+
  6. graph summarization
  7. t-norm: t-norm is a binary algebraic operation on the interval [0, 1],
  8. MPE inference
  9. 共识优化 consensus optimization
  10. logic rules 逻辑规则，规则 rule：
  11. 一阶谓词逻辑：
  12. 原子命题：原子公式)
  13. 解释 interpretation：
  14. rule 的 grounding 数：
  15. ground rule: 基本规则

image-20200817235935237

image-20200818094838660

image-20200818094909425

image-20200818095543339

image-20200818095145583

image-20200818095205647

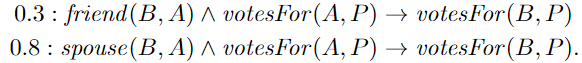
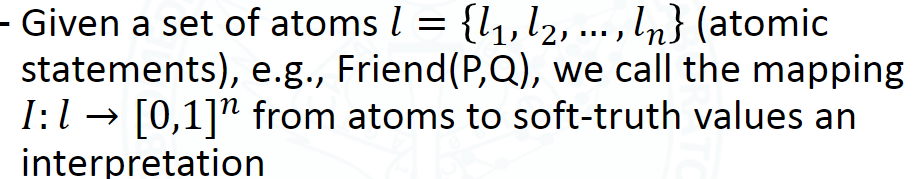
image-20200818104152253

image-20200818152654995

定义：

image-20200818155834481

image-20200818154410912

使得 Rules will behave like boolean logic (布尔逻辑用真值时，条件语句的真值表一致)

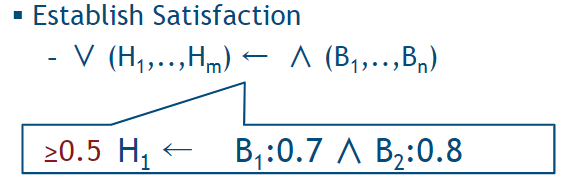
image-20200818153523164

satisfaction：左边ground atoms的值要大于等于 右边 atoms 的值

image-20200818153533540

image-20200818153629491

image-20200818160349166

详细查看：

Hinge-Loss Markov Random Fields and Probabilistic Soft Logic

slide1

slide2

slide3

  1. 可以为用户之间的不同类型的关系（例如友谊或家庭关系）建模，而且还可以对多种相似性概念
  2. ground out all rules：将predicate中的变量都用实例填充
  3. convert ground rules to hinge-loss functions
  4. constructing a HL-MRF
  5. making prediction

Abstract

概率软逻辑(Probabilistic soft logic PSL)是用于关系域 relational domains 中的 集体概率推理 collective, probabilistic reasoning 的框架。 PSL 将一阶逻辑规则 first order logic rules 用作图模型 graphical models 的模板语言 template language，该图模型针对区间为 [0, 1] 的具有软真值 soft truth values 的随机变量。在此设置下的推断是一项连续的优化任务 Inference in this setting is a continuous optimization task 。该文概述了 PSL 语言及其推理和权重学习技术 techniques for inference and weight learning 。

1 Introduction

人工智能中的许多问题都需要 处理关系结构和不确定性 relational structure and uncertainty 。因此，对促进具有关系结构的复杂概率模型 probabilistic models with relational structure 的开发的工具的需求不断增长。这些工具应将高级建模语言与通用算法相结合，以在最终的概率模型或概率程序中进行 推断 inference 。最近开发的框架，基于图模型，关系逻辑或编程语言的思想 graphical models, relational logic, or programming languages

作者概述了有关概率软逻辑（PSL 的最新工作。PSL模型已在各个领域开发，包括集体分类 collective classification，本体对齐 ontology alignment，个性化医学 personalized medicine，意见扩散 opinion diffusion ，对社交网络的信任 trust in social networks和图摘要 graph summarization。PSL 的主要区别特征是它在间隔[0，1]中使用软真值。This allows one to directly incorporate similarity functions,both on the level of individuals and on the level of sets. 例如，在社交网络中对意见 opinions in social networks 进行建模时，PSL不仅可以为用户之间的不同类型的关系（例如友谊或家庭关系）建模，而且还可以对多种相似性概念 multiple notions of similarity（例如基于爱好，信念或对特定观点的意见）进行建模。从技术上讲，PSL将感兴趣的域表示为逻辑原子 logical atoms。它使用一阶逻辑规则 first order logic rules 捕获域的依赖结构，并以此为基础在所有原子logical atoms上构建联合概率模型。每条规则 rule 都有一个相关的非负权重，可以捕获该规则 rule 的相对重要性。由于使用了软真值，PSL中的推理是连续优化问题。

下面介绍 PSL建模语言 及其 用于最可能的解释和边际推断 most probable explanation and marginal inference 的 高效算法的概述。

2 PSL Semantics

一个PSL程序由一组一阶逻辑规则组成，这些规则具有连接体 conjunctive bodies 和单个文字头 single literal heads 。每条规则 rule 都有一个相关的非负权重，可以捕获该规则 rule 的相对重要性。

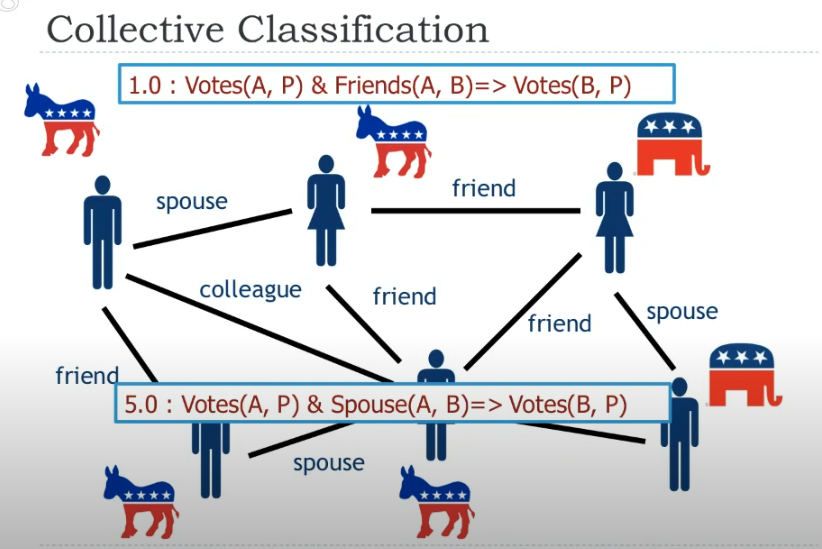
以下示例程序对 基于社交网络的简单模型 进行编码，以预测选民的行为，该社交网络具有两种表示朋友 friend 和配偶关系 spouse 的链接：

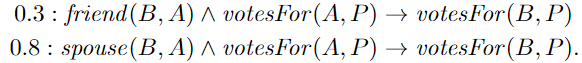
image-20200725162947109

上面的两条 first order logic rules ：从权重分配 认为 spouses are more likely to vote for the same party than friends

虽然PSL与一阶逻辑共享其 规则 的语法，但它使用来自位于 [0,1] 的 软真值，而不是仅使用0（false）和1（true）真值。Given a set of atoms $\ell=\{\ell_1,…,\ell_n\}$ 我们将映射 $I: \ell \rightarrow[0,1]^n$ 从 atoms 到 软真值 称为 解释 interpretation。 PSL 定义了 interpretation 上的概率分布 使得更有可能满足 更基本的规则实例 satisfying more ground rule instances——即在 interpretation 空间根据概率分布选择有利的，在上面的示例中，我们倾向于 一个人的投票结果会与朋友一致的解释 interpretation ，即 satisfies many groundings of 规则(1)，但在朋友和配偶之间进行权衡的情况下，由于较高的规则(2)的权重，投票上首选与配偶达成一致——即 “与配偶达成一致” 的 解释 interpretation 更好的满足 。

为了确定 基本规则 的满足程度 the degree to which a ground rule is satisfied，用 Lukasiewicz t-norm co-norm 分别作为 逻辑 AND 和 OR 的松弛形式， 这样的松弛在两端的值是确定的 0和1，但在中间提供连续的映射。

Given an interpretation $I$ , the formulas for the relaxation of logical conjunction (∧), disjunction (∨), and negation (¬) are as follows：

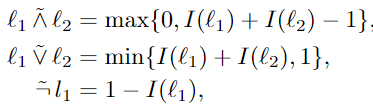
image-20200725171242551

符号上的波浪线指的是从 布尔域 的松弛。

对于 基本的PSL规则 a ground PSL rule $r\equiv r_{body} \rightarrow r_{head} \equiv \tilde \neg r_{body}\tilde\lor r_{head}$ (条件表达式性质)， 在 rule 中的 atoms上定义的 interpretation $I$ 将确定 r 是否满足要求，如果不满足，则说明其满足的距离 its distance to satisfaction。

Abusing notation， 我们将 $I$ 的使用范围扩大到 logical formulas。 logical formulas 公式的真值是通过从 $I$ 所指定的原子atom的真值开始 应用上述逻辑运算符的定义而获得的(命题逻辑？)(The truth value of a formula is obtained by applying the above definitions of the logical operators starting from the truth values of atoms as specified by $I$ 即上面通过应用 t-norm co-norm 得到的松弛后的逻辑运算符)

当给定一个 $I$， a rule $r$ is satisfied，也就是说 $I(r)=1$ (将 $I$ 的使用范围扩大到了 logical formulas上)当且仅当 $I(r_{body}) \le I(r_{head})$ ,也就是说 the head has at least the same truth value as the body. 同样，当真实值限制为0和1时，这与 rule satisfaction 的通常定义是一致的。 The rule’s distance to satisfaction under interpretation $I$ then measures the degree to which this condition is violated 这条 rule 到 satisfaction 的距离衡量了 该条件违背 satisfaction 的程度

举例：

考虑这个 Interpretation
$I=\{spouse(b,a) \mapsto 1, votesFor(a,p) \mapsto 0.9, votesFor(b,p) \mapsto 1\}$

$r$ 表示 the corresponding ground instance of 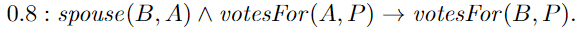image-20200726133404692

conjunction 松弛计算 $I(r_{body})=max\{0,1+0.9-1\}=0.9$

条件假设 松弛计算$d_r(I)=max\{0,0.9-0.3\}=0.6$

当 $I(r_{head})$ 的值大于或等于 0.9 则 距离为0

当给定 a set of ground atoms $\ell$ of interest，PSL 产生一个在可能的 interpretations $I$ 上的概率分布。

设 R be the set of all ground rules that are instances of a rule in the program。只在 $\ell$ 中有 atoms，$I$ 的概率密度函数 f 为

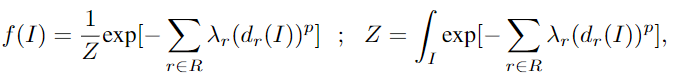
image-20200726175458909

其中 $\lambda_r$ 是 rule $r$ 的 权重，$Z$ 是 continuous version of the normalization constant used indiscrete Markov random fields, $p \in \{1,2\}$ 提供两种损失函数的选择

补充 indiscrete Markov random fields：

image-20200726180232206

线性损失函数（p = 1）倾向于 completely satisfy one rule 的 interpretations，但对于冲突规则而言，与 satisfaction 的距离要更远一些。而对于 平方损失函数 favors interpretations that satisfy all rules to some degree, which typically have truth values farther away from the extreme values

individual atoms $\ell_i$ 的值 通过 线性等式和不等式约束可以进一步限制。当出现违背这些约束时，我们设置 $f(I)=0$ ，并且限制 Z 的积分限 constrain the domain of integration for the normalization constant $Z$ accordingly.

这使人们可以编码其他领域知识 domain knowledge ，例如 a predicate being functional. 举例：在上面选民的例子中，每个选民 $a$ 不能投票超过一个参与党派 $p_1,p_2,…,p_n$，这就给了函数 $votesFor(.,.)$ 添加了约束

3 Inference and Learning in PSL

PSL 为以下两项关键任务提供了有效的推论 inference 方法

  1. MPE inference: 根据证据变量的取值，输出未知变量各种取值的概率
  2. 计算边际分布 computing marginal distribution

PSL程序的形式以及软真值的使用 可确保 非零密度nonzero density的解释空间interpretations space 形成 凸多面体 convex polytope。两种设置的推理算法都利用 凸的性质 来实现效率。此外，PSL还提供了从标记数据中学习权重的方法。我们在这里总结了主要思想，并参考相应的技术文章以获取完整详细信息

MPE Inference

  1. PSL中的第一个常见推理任务是 find the most probable interpretation given evidence (MPE)，即，拓展给定部分解释 partial interpretation 下最有可能得到的解释 interpretation。这意味着最大化等式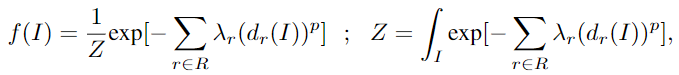image-20200726191002638中的密度函数 $f(I)$，这等效于最小化指数的求和，同时要满足 the evidence 以及 等式不等式约束。例如，在投票的例子中，给定社交网络和在民意测验中获得的少数人的真实投票行为，MPE推论得出所有其他人中最有可能的投票行为。
  2. 如 Broecheleret 等人[4]所示，可以将此约束优化问题转换为二阶锥规划 second order cone program（SOCP）。The SOCP can be solved in time $O(n^{3.5})$, where n is the number of relevant rule groundings, that is, those with non-zero distance to satisfaction. 为了避免操纵 avoid manipulation 不相关 的规则，PSL 遵循一种迭代方法，在构造SOCP之前，根据 evidence atoms 的真值 和非证据原子的当前真值确定一组相关规则 the set of relevant rules 。最初，真值0用于非证据原子。在构造并求解了 SOCP 之后，根据当前的MPE interpretation 更新相关规则集。重复此过程，直到不再激活任何规则 no more rules get activated.
  3. 最近，Bachet等人证明了基于 共识优化 consensus optimization 的 MPE推理 可以实现线性可扩展性 linear scalability ，同时其准确性仅比上述方法中使用的标准立方时间 SOCP solvers略低。共识优化 将优化问题 分解为 由其他约束联系在一起的独立的小问题。 在 PSL 中，separate subproblems are created for each ground rule。每个 此类子问题 都使用其自己的本地文字副本 own local copies of literals，并引入了约束，这些约束将这些本地副本的真值与相应原始文字的真值等同 equate the truth values of these local copies with those of the corresponding original literal。例如，对于a given person $a$ and party $p$，all groundings of 规则（1）和（2）在原始优化问题中都依赖于 $votesFor(a,p)$，但是通过在共识优化中使用该原子的不同副本而独立。共识优化然后在（a）优化本地副本的真值作为在最小化它们对原始目标的贡献以及与原始原子的同意之间进行权衡(minimizing their contribution to the original objective and their agreement with the original atom) 和 （b）将原始原子的真值更新为它们的本地副本的平均值，其中所有子问题均具有闭式解 之间 迭代

Computing Marginal Distributions

The second common inference task in PSL ：

计算 $P(l\le I(\ell_i)\le u)$ 即 一个 atom $\ell_i$ 从给出的区间 $[l,u]$ 取得一个真值的概率。

Broecheler和Getoor [3]引入了一种采样算法 sampling algorithm 来近似这种边际分布 marginal distributions ， 一般来说，这是一个 #P-hard problem in the number of ground atom。

直观地来说，计算这个概率 corresponds to computing the volume of the corresponding slice of the convex polytope of non-zero density interpretations. 对应于计算非零密度解释的凸多面体的相应切片的体积。

在PSL中，边际分布 marginal distributions 是通过 hit-and-run Markov chain Monte Carlo scheme(命中并运行的马尔可夫链蒙特卡洛斯) 后 收集采样点的直方图来估算的。 从如上所述有效地获得的 MAP状态 开始，算法首先通过随机 均匀地采样 一个方向，然后在该多面体内的 线段line segment上 采样一个点来探索凸多面体。由于一般方案可能会卡在多面体的拐角处 get stuck in corners of the polytope，在拐角处大多数方向都不指向多面体内部，这些情况是可以检测到，应用松弛方法将 方向采样限制为仅在可行方向采样

Weight Learning

可以通过最大似然估计来学习规则的权重 the weights of rules

对数似然 对 weight $\lambda_i$ 的梯度是：

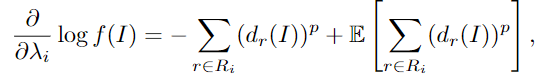
image-20200726204526494

image-20200726204549896

总结

细节上，PSL使用“软”逻辑作为其逻辑组成部分，以马尔可夫网络作为其统计模型。

概率软逻辑中的软逻辑指 逻辑结构真值不需要被严格的限制为0或1，可以是0-1之间的某个值

逻辑公式

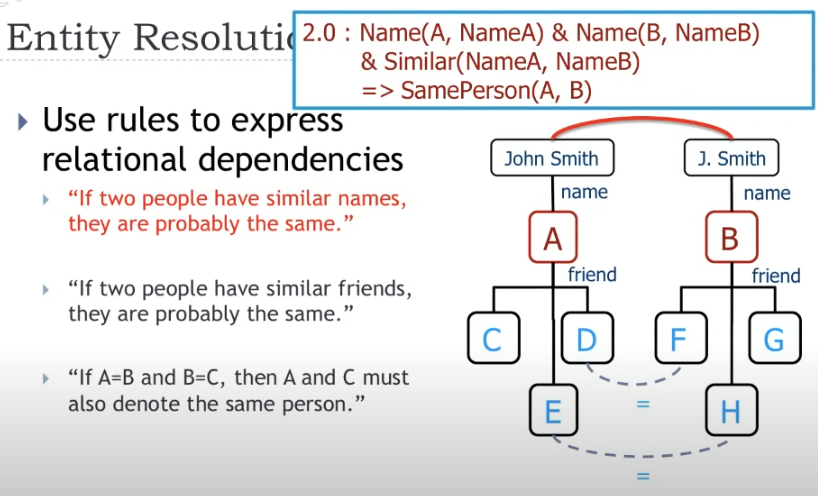
$similarName(X,Y) \rightarrow sameEntity(X, Y)$

它表达的逻辑意义可以理解为，如果X和Y具有相似甚至相同的name，那么我们可以说X和Y可能是同一个人，而 $similarName(X, Y)$ 的结果是0-1之间的某个值，具体的逻辑符号通过以下形式定义：

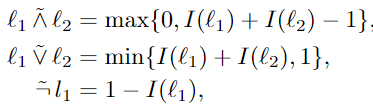
image-20200725171242551

在PSL模型中，这些具体的逻辑公式将成为马尔科夫网络的特征，并且网络中的每个特征都会与一个权重相关联，决定它在特征之间相互作用的重要性。权重可以手动设置或是基于已有真实数据通过学习算法学习得到。PSL还提供了复杂的推理技术，同时利用软逻辑的特点将知识推理的复杂度优化到多项式时间，而不再是一个NP-HARD问题

reference