『』阅读笔记
- 将rules 逻辑规则，论文中的是在网络中纳入约束。方式是通过将 包含逻辑比较符号以及合取析取求反的rules通过论文中给出的转化方式转化成几乎处处可微的损失函数。
- 将逻辑约束转换为具有所需数学特性的可微分损失函数 differentiable loss，基于标准梯度方法进行优化
- 用期望来建模，把最大化满足约束找到满足的输入集转化成最小化对约束的最大冲突，然后拆成内部的最大化目标，找到满足的输入集，再带入外部的最小化目标，优化网络的参数。
- 因为 3 中描述的第一步往往很难优化，因此对输入的变量 z 先投影到一个 convex set，而不是将变量是从convex set采样的作为constraint
code for DL2
project 地址
专有名词
projected gradient descent (PGD)
In mathematical logic, a literal is an atomic formula (atom) or its negation.
convex combination： 凸组合) Convex Combination of 3 point in R2 and Triangle
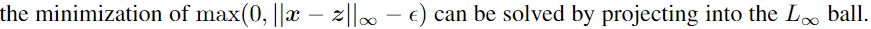(什么方法？)regression taskin an unsupervised setting, namely training MLP (Multilayerperceptron)
ABSTRACT
我们提出了DL2，这是一种用于训练和查询具有逻辑约束的神经网络的系统。DL2比以前的工作更具表现力，并且可以捕获对模型的输入，输出和内部的更丰富的约束 a richer class of constraints on inputs, outputs and internals of model。使用DL2，可以声明性地指定要在模型上训练 或 在查询期间要强制注入的领域知识，其目的是找到满足给定约束的输入。DL2的工作原理是将逻辑约束转换为具有所需数学特性的可微分损失函数 differentiable loss ，然后最小化该损失，基于标准梯度方法。
1 INTRODUCTION
一个关键挑战是使神经网络更可靠 reliable。解决这一挑战的可行方向是在培训过程中纳入约束条件 incorporating constraint（Madry等人，2017; Min-ervini等人，2017），并通过执行具体查询来检查已经受过训练的网络（Goodfellowet等人，2014b; Pei等人，2017;徐等人，2018））。尽管这些方法很有用，但它们被描述并硬编码 described and hardcoded 为特定种类的约束，从而使其难以应用于其他环境。
受先前工作的启发（例如，Cohen等人（2017）; Fu＆Su（2016）; Hu等人（2016））; Bach等人（2017）），我们引入了一种新的方法和系统，称为DL2（具有可微分逻辑with Differentiable Logic)的深度学习的缩写），可用于
- 查询网络中满足约束条件的输入，
- 训练网络以满足逻辑规范 logical specification，所有这些都是声明式的
我们的约束语言 constraint language 可以使用求反，合取和析取negations, conjunctions, and disjunctions 在神经网络的输入，神经元和输出上表达算术比较arithmetic comparisons 的丰富组合。得益于它的表现力，DL2使用户能够在训练期间加强领域知识或与网络进行交互，以便通过查询来了解其行为
DL2通过将逻辑约束转换为具有两个关键属性的非负损失函数来工作：
- （P1）损失为零的值可以保证满足约束条件，
- （P2）损失函数 都是可微分的。
这些属性相结合，使我们能够通过使用 现成的优化器 将损失降到最低 来 解决带有约束的神经网络 的 查询或训练的问题。
Training with DL2
为了使优化易于处理，我们排除了捕获凸集的输入约束，并将其作为优化目标的约束。我们使用投影梯度下降进行优化 projected gradient descent (PGD)，该方法在进行具有鲁棒性约束robustness constraints的训练是成功的(Madryet al., 2017). DL2的表现力以及通过PGD进行的易于处理的优化使我们能够训练新的有趣约束，比如：我们可以表达对概率的约束，而网络无法明确计算这些内容
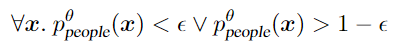
上面这个约束，在CIFAR-100的背景下，对于任何网络输入 x（网络由θ参数化），$people$ 的概率 $p_{people}$ 很小或很大。但是，CIFAR-100没有 $people$ 这个类别，因此我们将其定义为 a function of other probabilities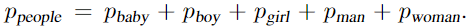 
我们显示，在类似的约束条件下（但有20个类），DL2在半监督的情况下提高了CIFAR-100网络的预测精度.
DL2 可以捕获在分类和回归任务中产生的约束。例如， GalaxyGAN （Schawinski等人，2017）要求网络遵守底层物理系统施加的约束，例如 通量flux：输入像素之和应等于输出像素之和。现在可以使用DL2，用声明性的方式表示为：$sum(x)= sum(\text{GalaxyGAN(x)})$，而不是将这种约束硬性地硬编码到网络中。
Global training
DL2的一个突出特点是它能够训练对输入施加限制的约束 outside the training set
先前关于约束训练的工作（例如Xu等人（2018））专注于给定的训练集，以对网络进行本地训练 local training以满足约束。使用DL2，我们可以首次 query for inputs which are outside the training set, and use them to globally train the network .
在 examples outside the training set 上进行训练的先前方法要么针对特定任务量身定制（Madry等，2017），要么针对网络类型（Minervini等，2017）。
我们的方法将全局训练的任务划分为：（i）优化器，它训练网络满足对输入的约束 the constraints for the given inputs，以及（ii）oracle，它为优化器提供旨在违反约束的新输入，考虑以下 Lipschitz 条件：
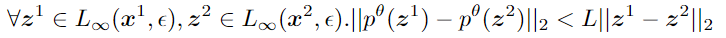
上式说明，对于训练集中的两个输入 $x^1,x^2$ ，在其 $\epsilon$ - neighborhood $(z^q,z^2)$ must satisfy the condition
如果满足Lipschitz条件，则神经网络会更稳定。
Querying with DL2
我们还设计了一种类似于SQL的语言，该语言使用户能够通过声明式查询posing declarative queries 来与模型进行交互。例如，考虑一下近期工作研究的场景（Song等人，2018），其中作者展示了如何使用AC-GAN生成对抗性示例（Odena等人，2016）。生成器用于从某个类别（例如类别1）创建图像，而该图片会混淆分类器（例如分类为7）。对于DL2，这可以表述为：
This query
aims to find an input $n\in \Bbb{R}^{100}$ 满足两条约束：
- domain constraint： 100维的 n 的每个元素都是在 -1 和 1 之间
- ACGAN输出的结果是 本应该是类别 1 由 $\text{M_ACGAN_G(n,1)}$ 约束， 但 NN 分类的结果是 类别7 $\text{M_NN1}$ 的输出结果是 7
DL2自动将此 query 转换为 DL2 的 loss，并使用现成的优化器（L-BFGS-B）对其进行优化以找到solution，在这种情况下为右侧的图像。
我们的语言可声明性地表述先前的许多工作，包括发现对给定预测负责 neurons responsible for a given prediction的神经元（Olah等人，2018），区分两个网络的输入（Peiet等人，2017）以及对抗性示例生成（例如Szegedy等人）等（2013年））
Main Contributions
2 RELATED WORK
Adversarial example generation 以看作是 as a fixed query to the network，while adversarial training (Madry et al., 2017) aims to enforce a specific constraint
大多数工作旨在 ，train networks with logic impose soft constraints, 通过添加 an additional loss(正则项？) (Pathak et al., 2015; Xu et al., 2018)。
(M ́arquez-Neila et al., 2017) 表明硬约束比软约束没有经验优势。
Probabilistic Soft Logic (PSL) (Kim-mig et al., 2012) translates logic into continuous functions over[0,1]. 如我们所示，PSL不易于进行基于梯度的优化，因为梯度很容易变为零。
Hu et al. (2016) builds on PSL and presents a teacher-student framework which distills rules into the training phase。 idea is to formulate rule satisfaction as a convex problem with a closed-form solution (对teacher network 的 输出分布 直接通过闭式解给出 避免对网络参数的训练)。然而，这种 formulation构造的公式 仅限于关于随机变量的rules，而不能表达关于概率分布的rules。但 DL2可以表达这样的约束，例如 $p_1>p_2$ 这要求类别1的网络输出概率大于类别2，而且，网络输出中 rules 的 线性性 导致的 凸性和闭式解 也是如此，这意味着非线性约束（例如，Lipschitz条件，可以用DL2表示）根本上是该方法无法实现的。
- work of Xu et al. (2018) 还限制于对随机变量的约束，对于复杂的约束是棘手的。
- Fu & Su (2016) reduces the satisfiability of floating-point formulas 转换成了数值优化，但是，它们的损失函数 不可微分，并且不支持对 分布 的约束。
- 没有先前的工作支持 回归任务 的约束
3 FROM LOGIC TO A DIFFERENTIABLE LOSS
Logical Language
包含 quantifier-free constraints， 可以用 conjunction (∧), disjunction (∨) and negation (¬) 来构造。
Atomic constraints (literals) 是比较符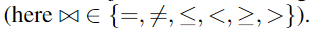
这些比较符 是用于标量的，逐元素应用于矢量。
不支持 量词 (quantifier-free constraints)
A term $t$ is : 对 t 的约定
Translation into loss
把约束转化成损失函数形式，损失函数中的 变量间 逻辑运算符 再做 translation
The translation rules：
比较符 $= \le$ 用距离函数来表示，L为0则表示满足约束，两元的比较符用 一个 连续的 可微的 scalar 表示
函数 $d$ 是就是对 逻辑比较符号的 translation，在论文的实现中，使用的是 absolute distance $\lvert t^1-t^2\rvert $ (因为是标量值，所以距离的度量直接是曼哈顿距离)
其余的比较符号：
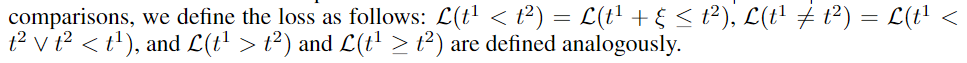
合取析取的 translation：
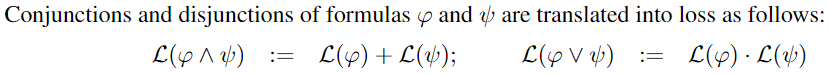
当两个 formula 都满足时，loss 为0，则两个 formula 的 合取式 也满足， loss 为0
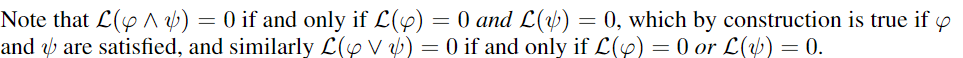
Translating negations
包含 Negations 的 constraints 被重写为 不包含 Negations 的 等价 atomic constraint (note that6=is not a negation).
对于 逻辑比较符
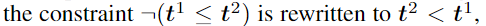
对于 合取析取符，
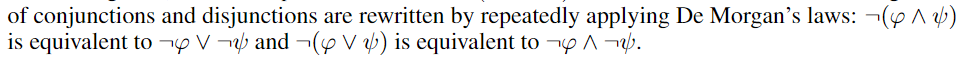
实例 $\bar x$ 带入 formula $\varphi$ 后使得 loss $L=0$ 则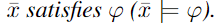 
当 loss 大于 一个 渐进于0的变量时，not satisfy
4 CONSTRAINED NEURAL NETWORKS
在本节中，我们介绍了用于训练具有约束条件的神经网络的方法。我们首先定义问题，然后提供 min-max formulation，最后讨论如何解决问题
$[\varphi]$ 是 指示函数： 1 if the predicate holds and 0 otherwise
Training with constraints
为了使用单个约束进行训练，我们考虑神经网络权重上的以下最大化问题，取值在[0,1]，最大为1
多个 constrain 的组合，通过 凸组合把 constrain 各自对应的 最大化期望问题组合起来
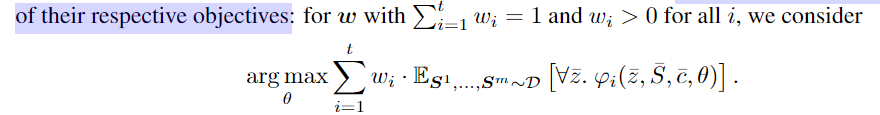
S 为 从训练集中 采样样本
Formulation as min-max optimization
对上面的式子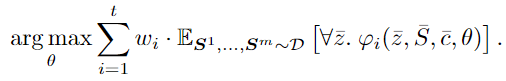
不直接求解这个最大化的优化问题，而是转变成
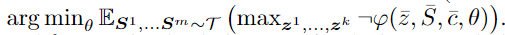最小化不满足约束概率的优化问题，这样可以将这个优化问题拆成两个子优化问题
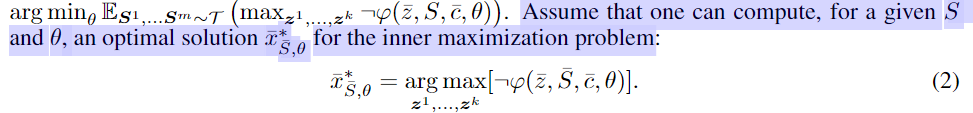
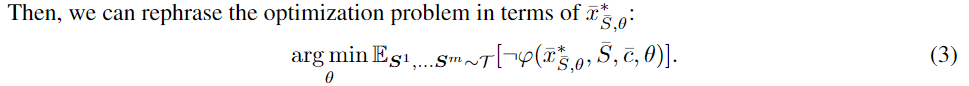
先找到最大化冲突，即最大不满足约束的实例 $\bar x$ ，然后在已知 $\bar x$ 的条件下，求最小化该情况的期望值
Solving the optimization problems
求解上面两个式子，通过第三节的方法 把 logical constraints 转换成 differentiable loss
对于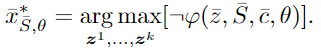
我们将其 translate 到 损失函数 loss $L$ 。最大化满足 约束的逆，即让满足 约束的逆 的损失 $L$ 最小： 根据 theorem1，
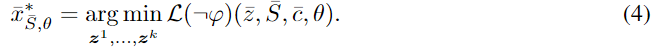
从上式解出 $\bar x$ 后，要使得在 约束 $\varphi$ 下出现 满足 约束的逆 的概率越小，所以要最小化下面的 损失函数
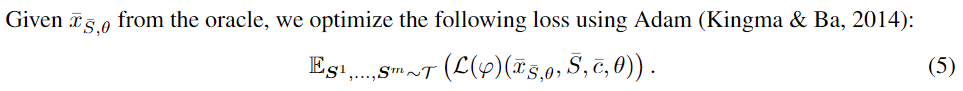
Constrained optimization
通常，（4）中的损失有时可能难以优化，
举例：
首先对 $\varphi$ 取反，$\le$ 根据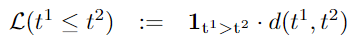
转成
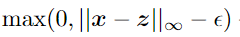
$\land$ 转成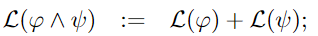 
这个式子很难优化，因为 the magnitude of the two terms is different，根据Carlini＆Wagner（2017）的报道，这导致 一阶方法 以过于贪婪的方式仅优化了单个项。
但是，某些约束具有闭式的解析解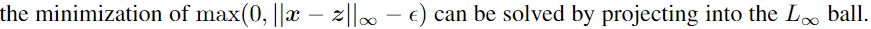，为此，我们确定了逻辑约束，这些约束将变量限制为具有有效投影算法的凸集，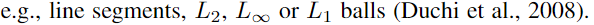
.
算法流程：
我们首先从训练集中形成随机样本的 mini-batch，the oracle 找到上面 式 6 的一个解，在将该解给 optimizer来 solve 式 5。请注意，如果φ没有变量（k = 0），即只有一个 constrain 则 oracle 将变平凡，直接计算 loss
5 QUERYING NETWORKS
我们以DL2为基础，设计了一种用于 查询网络querying networks 的声明性语言。先前工作中研究的硬编码问题现在可以用DL2查询表述：发现对给定预测负责 neurons responsible for a given prediction的神经元（Olah等人，2018），区分两个网络的输入（Peiet等人，2017）以及对抗性示例生成（例如Szegedy等人）等（2013年））
我们支持以下类别的查询：
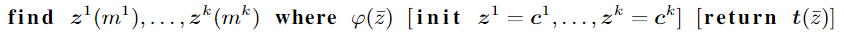
我们注意到用户可以用我们的语言指定 张量tensors（我们不假定它们被简化为矢量）。查询时，我们用逗号（，）表示连词（∧）； in 表示框约束 box-constraints，而 class 表示约束 目标标签target label，这被解释为对标签概率labels’ probabilities的约束
举例 几个有趣的查询。：
他的前两个是通过为CIFAR-10训练的网络定义的，而最后一个是针对MNIST的
The first query is to find an adversarial example $i$ of shape(32,32,3), classified as a truck (class9) ，$i$ 到 a given deer image(deer) 的距离在 6 到 24 间(距离用 $L_{\infty}$ 计算A)
目标是 找到 $i$ classified as a deer where a specific neuron is deactivated.
目标是 找到 $i$ classified differently by two networks where part of $i$ is fixed to pixels of the image nine
Solving queries
与训练一样，我们将 约束 编译为 损失loss，但是与训练不同，我们使用 L-BFGS-B 进行优化。虽然训练需要在PGD优化中分批输入，但查询却需要分配，因此有更多的时间使用更复杂但更慢的L-BFGS-B。我们将在附录C中讨论进一步的优化
6 EXPERIMENTAL EVALUATION
现在，我们对DL2在查询和训练具有逻辑约束的神经网络的有效性方面进行了全面的实验评估。我们的系统在PyTorch中实现（Paszkeet等，2017），并在Nvidia GTX 1080 Ti和4.20 GHz的Intel Core i7-7700K上进行了评估
6.1 TRAINING WITH DL2
我们评估了DL2在以下四个数据集上的各种任务（有监督，半监督和无监督学习）上：MNIST，FASHION（Xiao等人，2017），CIFAR-10和CIFAR-100（Krizhevsky＆Hinton，2009）。在所有实验中，约束条件之一是交叉熵（请参见第4节），以进行优化以提高预测精度。对于每个实验，我们都描述了其他逻辑约束
Supervised learning
考虑两种 约束
- global constraints，包括z-s,：
- training set constraints ： the only variables are from the training set (no ·z-s).
we write random samples (the S-s) $x_i$ : inputs from the training set $y_i$ : corresponding label
For local robustness (Szegedy et al., 2013)
training set constraint
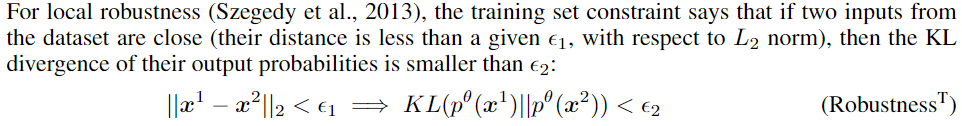
Global constraint
可能指的就是
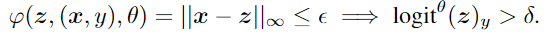
同样的，have two definitions for the Lipschitz condition.
training set constraint
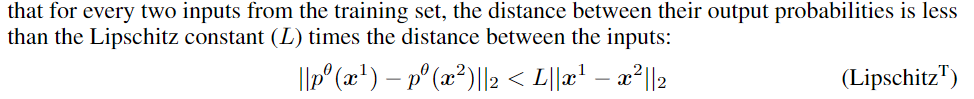
global constraint
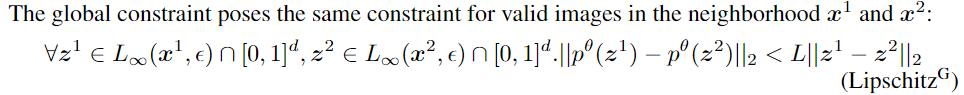
Imposing domain knowledge
training set constraint
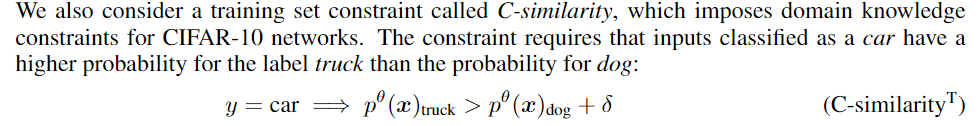
global constraint
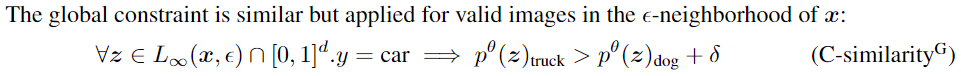
最后，我们考虑一个细分约束，它要求如果输入zi在位置λ上的两个输入x1和x2之间的直线上，则其输出概率在输出概率之间的直线上的位置λ上
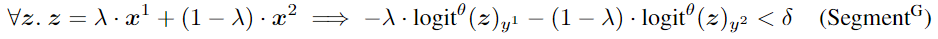
预测精度（P）和约束精度（C）
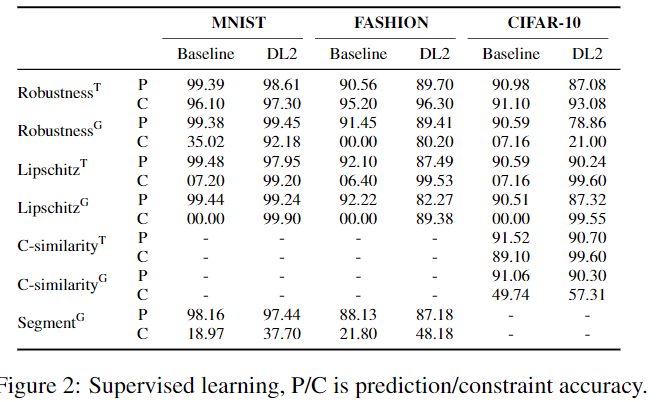
(i) crossed-entropy only (CE) and (ii) CE and the constraint.
P 预测精度略微下降， C 约束精度很高
Semi-supervised learning
我们将重点放在CIFAR-100数据集上，并将训练集按20/60/20的比例分为标记集，未标记集和验证集。
本着Xu等人的实验精神 Xu et al. (2018)，我们考虑约束条件 要求 类别组 groups of classes 的概率要么具有非常高的概率或非常低的概率。 A group consists of classes of a similar type( e.g., the classes baby,boy,girl,man, and woman are part of the people group), and the group’s probability is the sum of its classes’ probabilities
for a small $\epsilon$
我们使用此约束条件来比较几种方法的性能, we use the Wide Residual Network (Zagoruyko & Komodakis (2016)) as the network architecture.
Unsupervised learning
另外，我们约束 $d(0)=0$。接下来，我们以无监督的方式训练模型，使用DL2。在每个实验中，我们生成具有15个顶点的随机图，并将图分为训练（300），验证（150）和测试集（150）。作为无监督的基线，我们考虑一个始终预测 d（v）= 1的模型。我们还训练了具有均方误差（MSE）损失的监督模型。值得注意的是，我们的方法无需使用任何标签即可获得非常接近监督模型的错误。这证实了由DL2产生的损失可用于指导网络满足具有许多嵌套连接和分离的甚至非常复杂的约束。
6.2 QUERYING WITH DL2
我们评估了在TensorFlow中实现的具有约束的查询任务上的DL2。我们考虑了五个图像数据集，对于每个图像集，我们至少考虑了两个分类器。我们还考虑了生成器和鉴别器（使用GAN训练（Goodfellow等，2014a））。表3（附录E）提供了有关网络的统计信息。我们的基准测试包含18个模板查询 template queries（附录E），这些查询使用不同的网络，类和图像进行实例化。表1显示了结果（-表示不适用的查询）。 Queries ran with a timeout of2minutes.。结果表明我们的系统经常找到解决方案。尚未找到没有解决方案的查询是否具有解决方案是未知的。我们观察到查询的成功取决于数据集，例如，查询9-11对于除GTSBR之外的所有数据集都是成功的。这可能归因于GTSBR网络相对于这些查询旨在寻找的对抗示例的鲁棒性。利用区分词查找对抗示例的查询14仅对CIFAR数据集成功。可能的解释是，鉴别器是针对生成器创建的真实图像或图像进行训练的，因此，鉴别器在对仿生图像进行分类时表现不佳。利用生成器的查询15在所有经过测试的数据集中都成功，但是在每个数据集中只有很少的成功。至于整体解决时间，我们的结果表明，成功执行的过程会很快结束，并且我们的系统可以很好地扩展到大型网络（例如ImageNet）。
7 CONCLUSION
AND APPENDIX