Guo Jiazhen's Blog
0%

What Uncertainties Do We Need in Bayesian DeepLearning for Computer Vision?

Posted on Edited on In , , Views: Valine:
Symbols count in article: 7.9k Reading time ≈ 7 mins.
利用蒙特卡洛dropout来对认知不确定性进行建模，损失函数进行 MAP推断 从而对偶然不确定性进行建模

『What Uncertainties Do We Need in Bayesian DeepLearning for Computer Vision?』阅读笔记

专有名词

逐像素语义分割 综述解析

Abstract

可以建模的不确定性有两种主要类型：偶然事件不确定性（Aleatoric Uncertainty）捕获观测中固有的噪声(不可约)。另一方面，模型的不确定性说明了模型中的认知不确定性Epistemic Uncertainty-如果有足够的数据，就可以解释不确定性。传统上，很难对计算机视觉中的认知不确定性进行建模，但是现在有了新的贝叶斯深度学习工具，这是可能的。我们研究了在视觉任务的贝叶斯深度学习模型中对认知不确定性（Epistemic Uncertainty）与偶然事件不确定性（Aleatoric Uncertainty）建模的好处。为此，我们提出了一种贝叶斯深度学习框架，将输入依赖input-dependent的偶然不确定性 与 认知不确定性相结合。我们在具有逐像素语义分割和深度回归任务的框架下研究模型。此外，我们明确的不确定性公式 explicit uncertainty formulation 产生这些任务的新损失函数，这可以解释为学习衰减 learned attenuation。这使得损失对噪声数据的鲁棒性更高，还为分割和深度回归基准提供了最新的最新结果。

1 Introduction

很多机器学习算法可以很好地将高维空间的数据映射成低维数组，但很少考虑这些映射的准确率，从而导致很多灾难性的后果。

计算机视觉应用程序中的不确定性量化可以大致分为诸如regression settings such as depth regression, and classification settings such as semantic segmentation。在计算机视觉的这种设置中，对不确定性进行建模的现有方法包括粒子滤波和条件随机场 particle filtering andconditional random fields。大多数深度学习模型都无法表示不确定性。深度学习在现有的回归设置中不能表示不确定性，深度学习分类模型通常会提供归一化的分数向量，(softmax输出向量)无法捕获模型不确定性。对于这两种设置，都可以使用贝叶斯深度学习方法捕获不确定性，这为理解深度学习模型的不确定性提供了实用的框架[6]。

在贝叶斯建模中，可以对模型进行建模的不确定性有两种主要类型[7]。Aleatoric uncertainty，这可能是传感器噪声或运动噪声，从而导致不确定性，即使要收集更多的数据也无法降低不确定性。另一方面，epistemic uncertainty 是模型参数中的不确定性——这抓住了我们对哪个模型产生了对我们收集的数据的无知。如果有足够的数据，就可以解释这种不确定性，它通常被称为模型不确定性。Aleatoric uncertainty可以进一步分为同方差不确定性：对不同输入保持不变的不确定性和异方差不确定性；异方差不确定性取决于模型的输入，其中一些输入可能比其他输入具有更大的噪声输出。异方差不确定性对于计算机视觉应用尤其重要。例如，对于深度回归，具有强烈消失线的高度纹理化的输入图像预期会产生不自信的预测，而像无明显特征的墙 作为输入图像，预期会有非常高的不确定性

在本文中，我们观察到在许多大数据体系中(比如那些与图像数据有关的深度学习的体系)，建模偶然不确定性aleatoric uncertainty是最有效的——这类不确定性是不能被解释的。这是与认知的不确定性相比较，而认知的不确定性通常可以用机器视觉中大量的数据来解释。我们进一步证明建模 aleatoric uncertainty 是有代价的。数据外的例子，可以用epistemic uncertainty识别，不能单独用 aleatoric uncertainty 识别。

为此，我们提出了一个统一的贝叶斯深度学习框架，它允许我们从输入数据 映射到 aleatoric uncertainty，并将这些与epistemic uncertainty的估计组合在一起。我们推导了回归和分类应用的框架，并给出了逐像素深度回归和语义分割任务的结果(示例见图1和补充视频)。我们展示了如何在回归任务中建模aleatoric uncertainty，并可用于学习loss attenuation，并发展一个互补的方法为分类情况。这表明了我们处理困难和大规模任务的方法的有效性

贡献

  1. capture an accurate understanding of aleatoric and epistemic uncertainties, in particular with a novel approach for classification
  2. 通过减少噪声数据的影响，在非贝叶斯基线上提高模型性能1 - 3%，从明确表示偶然不确定性 explicitly representing aleatoric uncertainty 获得的隐含衰减 implied attenuation
  3. 我们通过刻画每个不确定性的性质并比较模型的性能和推理时间来研究建模 aleatoric or epistemic uncertainty 之间的权衡

现有的贝叶斯深度学习方法要么只捕捉认知不确定性，要么只捕捉偶然不确定性[6]。这些不确定性分别被表示为模型参数的概率分布或模型输出的概率分布。认知的不确定性是通过在模型的权重上放置一个先验分布来建模的，然后尝试捕捉给定一些数据的权重变化的多少。另一方面，偶然不确定性是通过 by placing a distribution over the output of the mode来建模的。例如，在回归中，我们的输出可能被建模为带有高斯随机噪声的。在这种情况下，我们感兴趣的是学习噪声的方差作为不同输入的函数(这种噪声也可以为所有数据点建模为一个常数值，但这没有意义)。这些不确定性，在贝叶斯深入的背景下，将在本节更详细地解释

2.1 Epistemic Uncertainty in Bayesian Deep Learning认知不确定性建模

Reference—Xieyuanli_Chen 的 cnblog

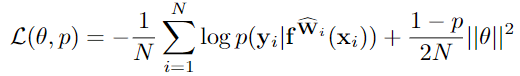
image-20200805225714888

为模型参数分布建模，$P(W|X,Y)$，通常通过网络模型参数的概率分布来研究认知不确定性，首先通过将先验分布置于模型的权重上进行建模，然后尝试计算这些权重随着数据变化的规律

在分类问题中，预测不确定性可以利用蒙特卡洛积分来近似

在回归问题中，这一认知不确定性可以通过预测方差来进行计算

2.2 Heteroscedastic Aleatoric Uncertainty异方差偶然不确定性计算

Reference—cnblog

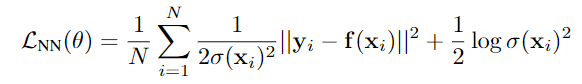
image-20200805225410026

MAP推断

研究网络输出来研究偶然不确定性，通常是对模型的输出进行拟合。例如在回归问题中，我们可以把输出建模为随着高斯随机噪声而衰减

计算回归问题中的偶然不确定性，我们需要对观测噪声参数 $\sigma$ 进行调整，计算异方差偶然不确定性，认为噪声的方差是不同输入的函数。

3 Combining Aleatoric and Epistemic Uncertainty in One Model

我们开发的模型将允许我们研究单独建模偶然不确定性、单独建模认知不确定性或在单个模型中同时建模这两个不确定性的影响。接着观察到回归任务中的偶然不确定性可以解释为学习损失衰减loss attenuation，这使得损失对噪声数据更加稳健。我们将异方差回归的思想扩展到分类任务。这也使我们能够了解分类任务的损耗衰减loss attenuation

3.1 Combining Heteroscedastic Aleatoric Uncertainty and Epistemic Uncertainty

为了同时捕捉认知和任意的不确定性，将§2.2中的异方差神经网络转换为贝叶斯神经网络，方法是将分布置于其权重之上。

我们需要推断一个BNN模型 $f$ 的后验分布，它将输入图像 x 映射到非随机输出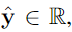image-20200805201612316，以及输出方差 $σ^2$ 给出的偶然不确定度的度量。我们使用 §2.1 中的公式，用一个 dropout变分分布 来近似BNN模型 $f$ 的后验分布。

结合BNN网络的随机输出分布的均值和方差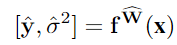：image-20200805224525673

image-20200805224759550

公式(第一张按照#2.1公式，第二张按照#3公式，两者一致，体现在权重表示为分布形式)：

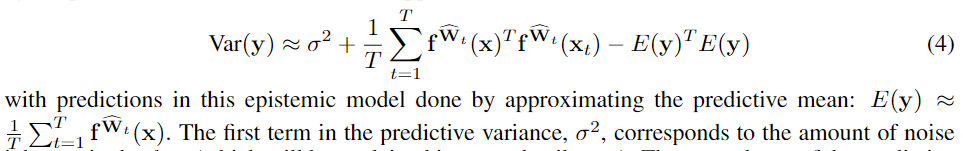
image-20200805225626828

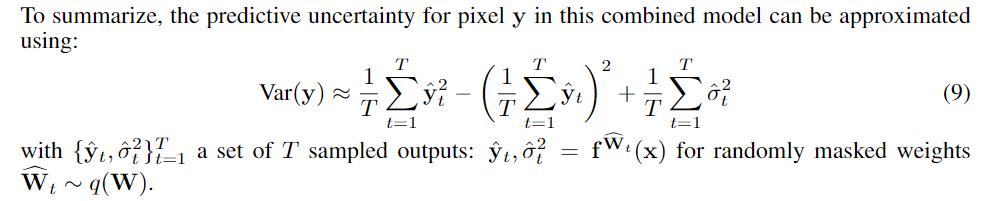
image-20200805234050251

建模偶然不确定性，第二项正则项防止第一项中的方差取极大：

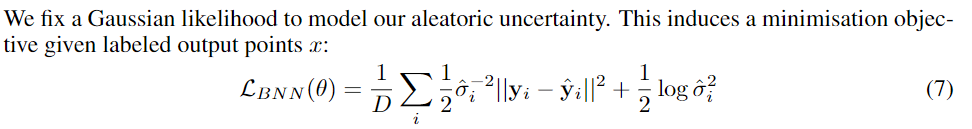
image-20200805225859353

加个对数避免了第一项除以零的数值不稳定性，

image-20200805231547566

combine 体现在将 #2.2 中 $f$ 固定的权重改成 概率分布，噪声方差的计算不同

3.2 Heteroscedastic Uncertainty as Learned Loss Attenuation

我们发现允许网络预测不确定性使得其可以通过 $exp(−s_i)$ 有效地减少损失残差(不确定性大时，会迫使第一项中的残差项减小)。这一行为与一个智能鲁棒的回归函数是类似的，它允许网络适应残差的权重，甚至允许网络学习减弱 错误标签 的影响 (错误标签，高不确定性为小权重)，这使得模型对噪声的鲁棒性增强：针对预测出高不确定性的输入，模型将对损失函数产生较小的影响。

这一模型不鼓励对所有的输入产生高不确定性——通过 $logσ^2$ 的形式实现 (正则项) ——因为会使得模型忽略这些输入。因此当高不确定性输入很多时将会对模型进行惩罚——即允许模型学会忽略数据，但会对其做出惩罚。这一模型同样不鼓励预测出不确定性低但残差高的结果，因为低 $\sigma^2$ 值会过于扩大残差的影响，同样会对模型进行惩罚。这种学习衰减不是一种特殊设计的结构，而是模型概率解释的结果——通过加正则项，以及建模出两个因素间的trade off来实现 Loss Attenuation

3.3 Heteroscedastic Uncertainty in Classification Tasks

分类中的异方差神经网络是一种特殊的分类模型，因为从技术上讲，任何分类任务都具有输入依赖的不确定性

  1. 在分类问题中，NN将会对每一个像素 $i$ 预测一个一元数组 $f_i$，当经过一个softmax运算后将形成一个概率数组 $p_i$

  2. We change the model by placing a Gaussian distribution over the unaries vector $f_i$ 把对每个 pixel $i$ 的unary vector $f_i$ 用一个 高斯分布随机变量替代：

    image-20200806113531761

    每个 $f_i$ indexed by i 都被注入了 方差为 $\sigma^W_i$ 的高斯噪声，即 Heteroscedastic Uncertainty

  3. 新模型的损失函数：对数似然

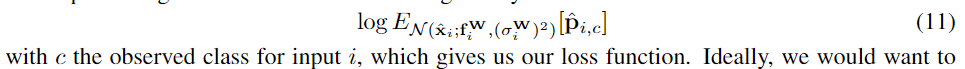
    image-20200806114448947

    求这个期望的时候，我们想将这个高斯分布解析地积分出来，但是没有解析解是已知的。我们采用蒙特卡洛积分来近似目标，sample unaries through the softmax function.。我们注意到这个操作是非常快的，因为我们只执行一次计算（将输入经过一次模型便可计算得到对数值）。我们只需要对softmax的输出进行抽样，这只是整个网络计算整体的一部分，因此并不会增加测试时的计算时间。因此数值稳定的损失函数如下所示，

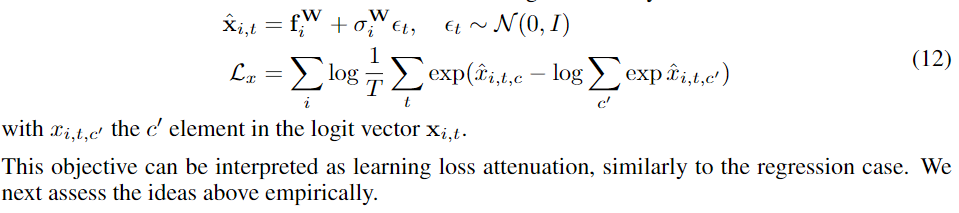
    image-20200806195558780

    这个损失函数形式变化，参考nameoverflow——Bayesian Neural Networks：贝叶斯神经网络，使得可以应用现有的优化方式

    image-20200806195540457

4 Experiments

本文在像素级的深度回归和语义分割问题上对所提出的模型进行了测试。为了展示本文所提出的可以学习的损失衰减的鲁棒性（对不确定性建模的好处之一），我们在CamVid, Make3D和NYUv2 Depth数据集上进行了测试，并取得了目前最好的性能。在实验中，我们利用了DenseNet的框架（用于深度回归问题），并对其稍微进行了改进（在CamVid上进行测试比改进前的性能提高了0.2%）。在所有的实验中，我们将训练图像裁剪成224x224，batch的大小为4，然后利用全尺寸图进行精调，batch大小为1，采用RMS-Prop优化方法，学习率为0.001，权值衰减率为10−410−4。我们利用蒙特卡洛dropout来对认知不确定性进行建模，DenseNet框架中采用的dropout概率为 $p=0.2$ ，在每一个卷积层后使用，本文中我们使用50个蒙特卡洛dropout采样。我们利用上文提到的损失函数进行 MAP推断 从而对偶然不确定性进行建模。在实际实验过程中，我们采用的是拉普拉斯先验(L1)而不是高斯先验(L2)，因为其采用的L1距离描述残差比高斯采用的L2距离更适合视觉回归问题

4.1 Semantic Segmentation

在此实验中，我们采用了CamVid和NYUv2数据集，其中CamVid是道路场景数据集包含367张训练图片以及233张测试图片，11个类别,实验结果如表一a所示，可以看出偶然不确定性对性能影响更大，结合两种不确定时系统性能最佳。NYUv2数据集是一个具有挑战的室内分类数据集，包含40中语义类别，实验结果如表一b所示。

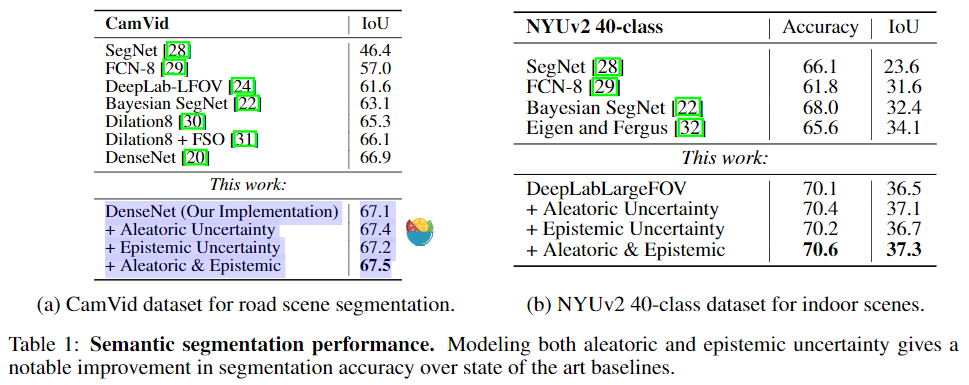
image-20200806201357626

mean intersection over union (IoU) score 显示：this application it is more important to model aleatoric uncertainty, suggesting that epistemic uncertainty can be mostly explained away in this large data setting.

4.2 Pixel-wise Depth Regression

在此实验中，我们采用了Make3D和NYUv2 Depth数据集，实验结果如表二所示，结果表明偶然不确定在此类问题中发挥了很大作用，如图五、图六所示，在图像深度较深，反射表面以及遮挡边界处large depths, reflective surfaces and occlusion boundaries in the image的偶然不确定性值很大，这些地方往往是单目深度算法容易失败的地方。反观由于数据量太少，认知不确定很难发挥大作用。总的来说，我们通过直接学习系统噪声和复杂概念的衰减从而提高了非贝叶斯网络的性能，例如我们观察到遥远物体和物体和遮挡边界的偶然不确定性是比较高的。

5 Analysis: What Do Aleatoric and Epistemic Uncertainties Capture?

在这一节中，我们希望研究建模偶然和认知的不确定性的有效性。特别地，我们希望量化这些不确定度测量的性能，并分析它们捕获了什么

5.1 Quality of Uncertainty Metric

在图二中我们给出了回归问题和分类问题的PR曲线，PR曲线说明了我们的模型性能可以通过消除不确定性大于方差阈值的像素来提高。这表示了不确定性的两种行为，一是不确定性测量与精度是相关的，因为所有曲线都是严格递减函数，当模型有更多不确定的点时，精度会降低；二是两种不确定性的曲线是相似的，在没有其他不确定性的情况下，每个不确定性对像素置信度的排序与其他不确定性相似，即使当只有一个不确定性能被建模时，它会在一定程度上弥补另一不确定性

在图三中我们用我们模型在测试集上的校准图分析不确定性度量。对于分类问题而言，我们通过将我们模型预测的概率离散化成一些数，然后画出正确预测的标注的频率对应的数，不确定性质量越高的预测应该与$y=x$更加接近。对于回归问题而言，我们可以通过比较预测分布的变化阈值内的残差频率来形成校准图we can form calibration plots by comparing the frequency of residuals lying within varying thresholds of the predicted distribution.

5.2 Uncertainty with Distance from Training Data

  1. 偶然不确定性无法通过更多数据解释。
  2. 偶然不确定性也不会因为与训练集不同的样本而增加，而认知不确定性会

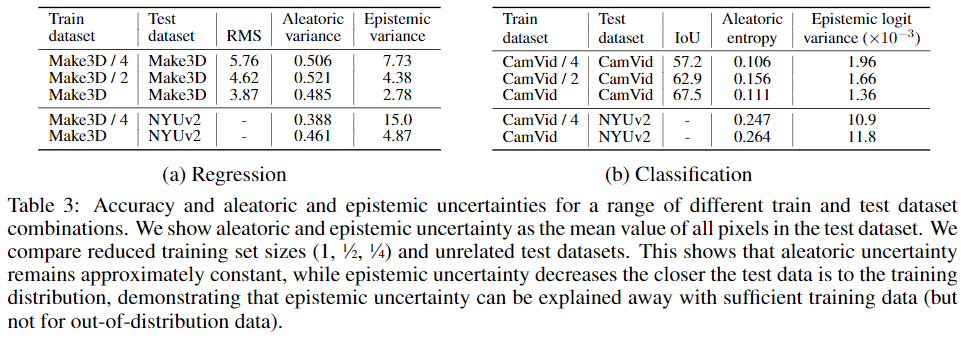
在表三中我们给出了在子集不断增加的数据上训练模型的精度与不确定性，结果表明认知不确定性将随训练集增大而减小，结果同时表明偶然不确定性保持相对稳定，不能被更多数据解释。利用不同的数据集进行测试时认知不确定性会稍微增加。

image-20200806204638776

5.3 Real-Time Application

偶然不确定性增加的时间可以忽略不计，认知不确定性蒙特卡洛采样是比较耗时的 ResNet只有最后几层有dropout需要采样，而denseNet require the entire architecture to be sample，因为CPU的显存限制

6 Conclusions

对以下情形计算偶然不确定性是比较重要的：

  1. 具有大量数据的情况，这种情况下认知不确定性是可以被解释的。
  2. 实时系统，偶然不确定性不会影响实时性。

对以下请性计算认知不确定性是比较重要的：

  1. 对安全性要求较高的应用，对uncertainty比较敏感的应用，因为认知性能可以识别出当前场景与训练集是否一致。
  2. 小数据集情况，training data is sparse时

偶然事件不确定性（Aleatoric Uncertainty）和 认知不确定性（Epistemic Uncertainty）

reference—深度学习中的两种不确定性

传统深度学习算法几乎只能给出一个特定的结果，而不能给出模型自己对结果的置信度。当输入不在训练集出现过的样本时，softmax输出概率不太可能是在标签集上的平均值如(0.5,0.5)原因

BNN (Bayesian Neural Network)。BNN的原理大体上是，我们网络中每个参数的weight将不再是一个特定的数字，取而代之的是一个先验分布。这样我们train出来的网络将不再是一个函数，而是一个函数的分布BNN详细

1 偶然不确定性

数据本来就存在误差。数据集里这样的bias越大，我们的偶然不确定性就应该越大。(来自数据收集过程的不可约减的噪声,这个现象不能通过增加采样数据来削弱，解决这个问题的方法一般是提升数据采集时候的稳定性，或者提升衡量指标的精度以囊括各类客观影响因素)

可以进一步分为同方差不确定性（Task-dependant or Homoscedastic uncertainty）和异方差不确定性（Data-dependant or Heteroscedastic uncertainty）

  • 异方差不确定性，取决于输入数据，并预测为模型输出。其中一些输入可能具有比其他输入更多的噪声输出。异方差的不确定性尤为重要，可以防止模型输出非常自信的决策
  • 同方差不确定性，不取决于输入数据。它不是模型输出，而是一个对所有输入数据保持不变并且在不同任务之间变化的数量。因此，它可以被描述为任务相关的不确定性
2 认知不确定性

认知不确定性测量的，是我们的input data是否存在于已经见过的数据的分布之中。(对真实模型的无知，模型自身对输入数据的估计可能因为训练不佳、训练数据不够等原因而不准确，与某一单独的数据无关。可以通过有针对性的调整（增加训练数据等方式）来缓解甚至解决的)

两种不确定性的量化

对于回归问题

1 认知不确定性的量化

估计数据集的真实分布 $P(D)$ $D$ 为数据集，$W$ 为权重

蒙特卡洛方法对网络参数的后验概率 $P(W|D)$ 进行估计，后验概率 $P(W|D)$ (我们就可以知道 $D$ 到底在不在我们已经学习的分布中，从而获得认知不确定性)

reference—贝叶斯深度学习-概述

R TALK | 旷视危夷晨：不确定性学习在视觉识别中的应用