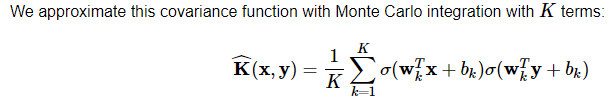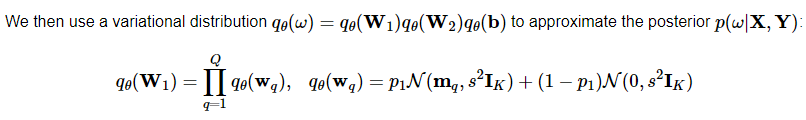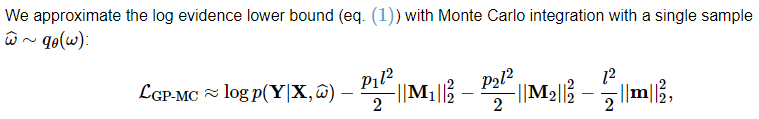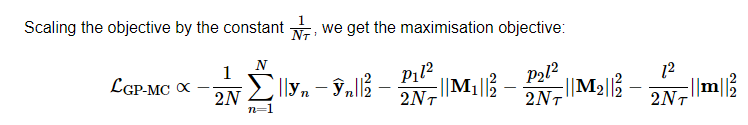『Dropout as a Bayesian Approximation Representing Model Uncertainty in Deep Learning』阅读笔记
后续工作——Inter-domain Deep Gaussian Processes with RKHS Fourier Features
Abstract
从 Bayesian 角度，解释了 why dropout works，以及如何对dropout神经网络的不确定性进行建模 。
深度学习工具的回归和分类不能捕捉模型的不确定性。在比较中，贝叶斯模型提供了一个数学基础框架来解释模型的不确定性，但计算成本高。
本文提出了一种新的理论框架，将深度神经网络中的dropout training as approximate Bayesian inference in deep Gaussian processes。这一理论的一个直接结果是使用dropout NNs 从现有的模型中提取不确定性。这在不牺牲计算复杂度或测试精度的情况下，减轻了representing uncertainty in deep-learning的问题。我们对dropout uncertainty的性质进行了深入的研究。以MNIST为例，在回归和分类任务上评估了各种网络结构和非线性。我们显示了一个相当大的改进在预测对数似然和RMSE相比前先进的方法，并完成我们的dropout uncertainty在深度强化学习的应用
1. Introduction
softmax输出不能表示为不确定性，普通模型优化目标得到的是参数的点估计，However, passing the distribution (shaded area 1a) through a softmax (shaded area 1b) better reflects classification uncertainty far from the training data：下图中对训练集外的数据给出预测为class 1，且给出很高的probabiliity值
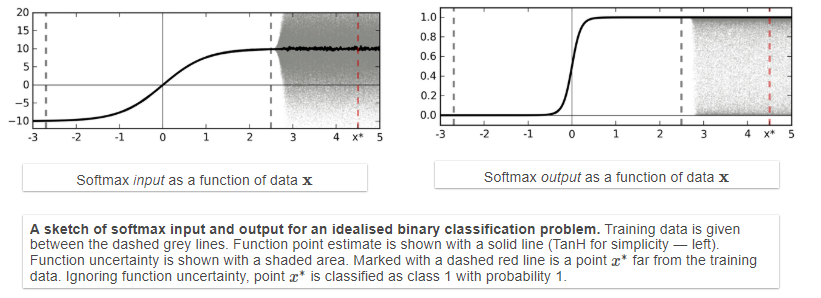
有了模型置信度，我们可以显式地处理不确定输入和特殊情况。例如，在分类的情况下，模型可能返回一个具有高不确定性的结果。不确定性在强化学习(RL)中也很重要。有了不确定性信息，agent就可以决定何时利用和何时探索其环境。
贝叶斯概率论为我们提供了基于数学的工具来推断模型的不确定性，但通常伴随着高昂的计算成本。也许令人惊讶的是，在不改变模型或优化的情况下，将最近的深度学习工具转换为贝叶斯模型是可能的。我们表明，在神经网络中使用dropout(and its variants)可以解释为高斯过程(GP)的概率模型。在深度学习的许多模型中，Dropout作为一种避免过度拟合的方法被使用，我们的解释表明dropout approximately integrates over the models’ weights。我们开发了一些工具来表示现有dropout神经网络的不确定性。
本文对高斯过程和dropout之间的关系进行了完整的论证，并开发了表示深度学习中不确定性的必要工具。我们在回归和分类的任务上，对dropout神经网络和卷积神经网路得到的不确定性的性质进行了广泛的探索性评估。本文以MNIST为例，比较了不同模型体系结构和非线性回归得到的不确定性，表明模型不确定性是分类任务不可缺少的。然后，与SOTA相比，我们在预测对数似然和RMSE方面显示了相当大的改进。最后，我们针对类似于深度强化学习的实际任务，对强化学习设置中的模型不确定性进行了定量评估。
2. Related Research
infinitely wide (single hid-den layer) NNs with distributions placed over their weights converge to Gaussian processes (Neal, 1995; Williams,1997). 因为带有 limit极限运算，所以一般研究 finite NNs s with distributions placed over their weights 一般称为 Bayesian neural networks，也为过拟合提供了鲁棒性，但challenging inference and additional computational costs.
最近的变分推理 sampling-based variational inference and stochastic variational inference ，这些已经被用来获得贝叶斯神经网络的新近似，表现得和dropout一样好t (Blundell et al.,2015). 然而，这些模型的计算成本高得令人望而却步。为了表示不确定性，对于相同的网络规模，这些模型中的参数数量增加了一倍。此外，它们需要更多的时间来收敛，也没有改进现有的技术。考虑到良好的非确定性估计可以从常见的dropout模型中廉价获得，这可能会导致不必要的额外计算。变分推断的另一种方法利用了 expectation propagation (Hern ́andez-Lobato & Adams, 2015) ，在RMSE评价和对 VI approaches的不确定性估计上有很可观的改进。
3. Dropout as a Bayesian Approximation
我们证明了具有任意深度和非线性的神经网络，在每个权重层之前都应用了dropout，在数学上等价于概率深度高斯过程 probabilistic deep Gaussian process的近似(Damianou &Lawrence, 2013)(在其协方差函数参数上的边际分布)。我们想强调的是，在文献中没有对dropout的使用进行简化，并且所推导出的结果适用于任何在实际应用中使用dropout的网络体系结构。此外，我们的结果也与dropout的其他变体相关联(比如drop-connect)，(Wan et al., 2013), multiplicative Gaussian noise (Srivas-tava et al., 2014), etc.).
结果表明，dropout，实际上，最小化了一个近似分布和一个deep Gaussian process的后验之间的 KL散度 (marginalised over its finite rank covariance function协方差函数 parameters)。
common dropout NN( non-probabilistic NN)
常见的最小化目标公式：
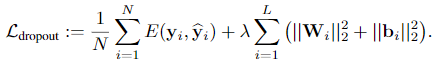
使用dropout，我们为每个输入点和每个层中的每个网络单元(除了最后一个)采样伯努利分布变量(为隐层创建一个mask，对每个隐变量为伯努利分布)。
deep Gaussian process
用于为新输入预测的公式
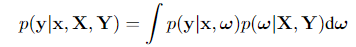
对于第二项 后验概率，采用变分近似
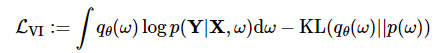
损失函数 第一项为普通 dropout NN的的最大似然估计损失，第二项为让替代的分布更接近
应用到高斯过程中：
参数方法需要推断参数的分布，而在非参数方法中，比如高斯过程，它可以直接推断函数的分布,allows us to model distributions over functions. 假设我们有一个协方差函数(核函数)：
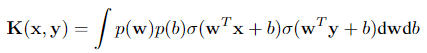
频谱分析?
详情见作者的博客What My Deep Model Doesn’t Know…中的Why Does It Even Make Sense?·
这个积分用 Monte Carlo integration 蒙特卡洛积分来近似
用了重参数化，使得可微：可结合nameoverflow的 zhihu blog
对 $q(W)$ 的形式，给出了一个混合尺度高斯先验（scale mixture gaussian prior）
对上面损失函数的第一项做近似，用 w 的一个点估计？蒙特卡洛积分的累加和 1/n抵消
scaling 防止 个数越多影响越大？可以证得这是前面损失函数的一个无偏估计，形式上已经可以看出是 dropout NN的经典损失函数形式 (对于回归问题而言)
从 Bayesian 角度，解释了 why dropout works。与dropout as noise regularization 很相似，approximation 也在引入 noise
4. Obtaining Model Uncertainty
对dropout NN 做 T 次前向传播，每次dropout 的权重都不同，数学表达即 T 组 mask：
对输出分布做一阶矩估计，求输出分布的期望，采用蒙特卡洛积分：
对输出分布做二阶矩估计，同样用蒙特卡洛积分：
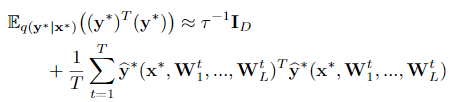
对输出的不确定性估计，在二阶矩的基础上还要减去一阶矩的平方：
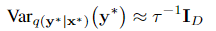
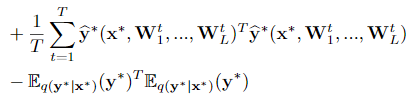
Gaussian process precision：
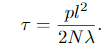
我们的预测分布 $q(y^∗|x^∗)$ 预计是高度多模态的，上面的近似只给出了它的属性的一个粗略的了解。这是因为在每个权重矩阵列上放置的近似变分分布是双模态的，因此在每一层的权重上的联合分配是多模态的(附录3.2节)。注意，dropout NN模型本身并没有改变。为了估计预测均值和预测不确定性，我们简单地收集随机正向通过模型的结果。因此，该信息可以用于现有的基于dropout训练的神经网络模型。此外，向前传播可以同时进行，在恒定的运行时间内完成，与标准 dropout一致
双模态 多模态说法可以看： 即 混合高斯先验模型和 dropout 的 伯努利分布 的混合
5. Experiments
接下来，我们在回归和分类的任务上，对从dropout NNs and convnets 中获得的不确定性估计的性质进行了广泛的评估。以MNIST (LeCun & Cortes, 1998)为例，比较了不同模型体系结构和非线性对分类任务的不确定性，表明模型不确定性对分类任务很重要。然后，我们表明，使用dropout的不确定性，我们可以在预测对数似然和RMSE log-likelihood and RMSE 方面取得相当大的改进，与现有的先进的方法。最后，我们以使用 model’s uncertainty in a Bayesian pipeline.
5.1. Model Uncertainty in Regression Tasks
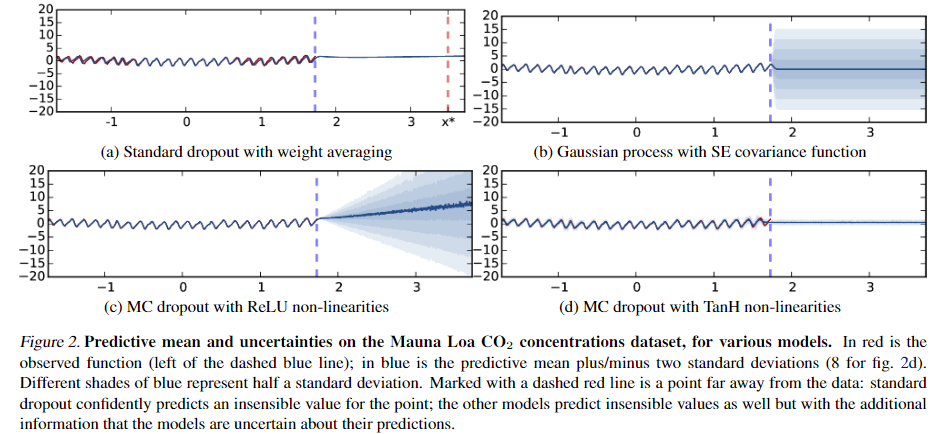
蓝色虚线右边是寻来你集外的数据，蓝色阴影部分different shades of blue represent half a standard deviation b、c两图表示模型输出的不确定性，d图输出零附近，也是输出了模型对结果的不确定性。
外推结果如图2所示。模型在训练数据(蓝色虚线的左边)上进行测试，并在整个数据集上进行测试。图2a显示了5层模型的标准dropout(即with weight averaging and without assessing model uncertaint)的结果。图2b显示了用平方指数协方差函数的高斯过程 Gaussian process with a squared exponential covariance function得到的结果。图2c显示了与图2a相同的网络的结果，但是使用了MC dropout来评估训练集和测试集的预测均值和不确定性。最后，图2d使用5层的TanH网络显示了相同的结果(为实现可视化目的，用8倍的标准偏差绘制)。蓝色的阴影表示模型的不确定性:每个颜色梯度colour gradient 表示半个标准偏差( 在预测平均值的正/负总共2个标准偏差内，代表95%的置信度 )。没有绘制的是具有4层的模型，因为它们收敛于相同的结果。
通过对观测数据的外推，没有一个模型可以消除这种周期性(尽管有了合适的covariancefunction，GP可以很好地捕捉到它)。标准的dropout NN模型(图2a)对point $x^∗$(用虚线标记)的值预测为0，具有很高的可信度，尽管这显然不是一个合理的预测。GP模型通过增加其预测的不确定性来表示这一点——实际上宣布预测值可能为0，但模型是不确定的。这种行为也在MC dropout中捕获。即使图2中的模型有一个不正确的预测平均值，增加的标准差表达了模型关于点的不确定性。请注意，ReLU模型的不确定性远远大于数据，而TanH模型的不确定性是有界的。图3。对于mcdropout模型的relnm -linear的Mauna loaco2浓度数据集的预测平均值和不确定性，近似于10个样本。
因为dropout的不确定性来自GP的属性，在GP中，不同的协方差函数对应于不同的不确定性估计。ReLU和TanH近似具有不同的GP协方差函数（附录中的第3.1节），TanH饱和，而ReLU不饱和。对于TanH模型，我们使用dropout概率0.1和dropout概率0.2来评估不确定性。最初以dropout概率0.1初始化的模型显示出的不确定性要比以dropout概率0.2初始化的模型要小，但是当模型converged the uncertainty后，接近优化的末尾几乎无法区分dropout概率的不同。dropout模型的矩收敛到近似GP模型的矩——它的均值和不确定性。值得一提的是，我们尝试将数据与层数较少的模型拟合失败。为进行绘图，用于估计不确定度（T）的正向迭代次数为1000。可以使用更小的数字来对预测平均值和不确定性进行合理估计（例如，图3，T = 10）
5.2. Model Uncertainty in Classification Tasks
为了评估模型分类的可信度，我们测试了一个在完整MNIST数据集上训练的卷积神经网络(LeCun & Cortes, 1998)。我们训练了LeNet卷积神经网络模型(Le-Cun et al.， 1998)，在最后一个完全连接的内积层(convnets中使用dropout的通常方式)之前使用dropout。dropout概率是0.5。我们使用相同的 learning rate policy训练了10^6个迭代的模型，就像之前使用的一样，使用的是(= 0.0001andp= 0.75)。我们使用Caffe (Jia et al.， 2014)作为本实验的参考实现。
我们用数字1的连续旋转图像(如图4的x轴所示)输入评估了训练后的模型，For the 12 images, the model predicts classes [11 1 1 1 5 5 7 7 7 7 7]
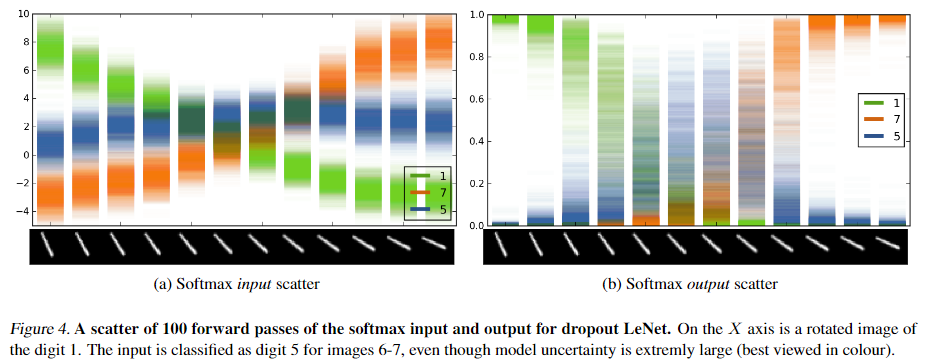
if the uncertainty envelopeintersects that of other classes (such as in the case of themiddle input image), then even though the softmax outputcan be arbitrarily high (as far as 1 if the mean is far fromthe means of the other classes), the softmax output uncer-tainty can be as large as the entire space
5.3. Predictive Performance
预测对数似然表示模型拟合数据的程度，数值越大表示模型拟合得越好。不确定性的质量也可以从这个数量来确定(见附录中的4.4节)。我们复制了Herńandez Lobato&Adams（2015）中的实验设置，并比较了RMSE和 predictive log-likelihood of dropout （在实验中称为“dropout ”）与概率反向传播 Probabilistic Back-propagation（称为“PBP”, (Hern ́andez-Lobato & Adams, 2015)到贝叶斯网络中的一种流行的变分推理技术(即“VI”，(Graves, 2011))。本实验的目的是 比较 在 naive 神经网络中应用 dropout 获得的不确定度质量 与 为获取不确定度而开发的专门方法的不确定度质量
根据我们对dropout的贝叶斯解释Bayesian interpretation of dropout(eq.(4))，我们需要定义一个先验的长度尺度，并找到一个optimal模型精度参数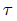
，该参数将允许我们评估预测对数似然(eq.(8))。我们使用Bayesian optimisation (BO, (Snoek et al., 2012; Snoek & authors,2015))在验证集的log-likelihood to find optimal 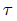，并设置 prior length-scale为 $10^{−2}$的大多数数据集基于数据的范围。请注意，这是一个标准的dropoutNN，其中，具体操作：
5.4. Model Uncertainty in Reinforcement Learning
强化学习一个agent从不同的状态得到不同的回报，它的目标是随着时间的推移使其期望的结果最大化。agent试图学会避免掉到rewards小的state，并选择能导致更好的state的action。在这项任务中，不确定性是非常重要的——有了不确定性信息，agent就可以决定何时利用其所知道的奖励，以及何时探索它环境。
最近RL的发展利用NNs来估计 agents’ Q-value functions（称为Q网络），这种函数可以估计不同行为的质量agent可以采取不同的状态。这导致了在Atari游戏模拟方面取得了令人印象深刻的结果，在这些模拟中，agents 在各种游戏中超过人的表现（Mnih et al.，2015）。在这个集合中使用了Epsilon贪心搜索Epsilon greedy search ，在这个集合中，智能体以一定的概率根据当前的Q函数估计选择最佳动作，否则进行解释。利用dropout Q-network给出的不确定性估计，我们可以使用诸如康普逊抽样（汤普森，1933）等技术来更快地收敛epsilon greedy并且avoiding over-fitting
我们训练了原始模型，并在每个权重层之前应用了一个概率为0.1的additional modelwith dropout。注意，为了进行比较，在这个实验中，两个agent使用相同的网络结构。在使用dropout的真实世界场景中，我们将使用一个更大的模型(因为原始模型被有意地选择为较小的以避免过度拟合)。为了利用dropout Q-network的不确定性估计，我们使用Thompson sampling而不是epsilon贪婪。实际上，这意味着每次我们需要采取action时，我们都会执行一个单一的随机正向通过网络 a single stochastic forward pass 。在回放中，我们执行一个随机正向传递，然后用抽样的伯努利随机变量进行反向传播。在appendix的第E.2节中给出了确切的实验设置